最长公共子序列

最长公共子序列（Longest Common Subsequence，LCS），是动态规划中的一个经典的问题，即求两个序列中最长的公共子序列（可以不连续）

动态规划

我们考虑从子状态进行转移，那么对于两个序列的最后一位来说，有以下两种情况

• 两个序列的最后一位元素相同
• 两个序列的最后一位元素不同

对于给定序列 $S1$ 和 $S2$，在最后一位元素相同的情况下，$LCS$ 的长度就是 $S1_{i-1}$ 和 $S2_{i-1}$ 的 $LCS$ 长度 + 1。（对于 $S1$ 和 $S2$ 的任何公共子序列来说，去掉最后一个元素后都是 $S1_{i-1}$ 和 $S2_{i-1}$ 的公共子序列

在最后一位相同的情况下，$LCS(S1,\ S2) = LCS(S1_{i-1},\ S2_{i-1}) + 1$

在最后一位元素不同的情况下，那么 $LCS$ 的长度就应该是取 $LCS(S1,\ S2_{i-1})$ 和 $LCS(S2,\ S1_{i-1})$ 中较大的那个，因为在最后一位元素不同的情况下，$LCS$ 中不可能同时包含这两个元素

在最后一位元素不相同的情况下，$LCS(S1,\ S2) = max(LCS(S1,\ S2_{i-1}),\ LCS(S2, S1_{i-1}))$

$$ LCS(S1,\ S2) = \left\{ \begin{array}{l} LCS(S1_{i-1},\ S2_{i-1}) + 1 & &\ S1_i = S2_i \\ max(LCS(S1,\ S2_{i-1}),\ LCS(S2, S1_{i-1})) & &\ S1_i\ !=\ S2_i \end{array}\right. $$

考虑维护一个数组 dp[][]，dp[i][j] 表示 $S1$ 的前 $i$ 位和 $S2$ 的前 $j$ 位的 $LCA$，进行动态规划

代码实现

for (int i = 1; i <= n; ++i)
{
    for (int j = 1; j <= n; ++j)
    {
        if (a[i] == b[j])
            dp[i][j] = dp[i - 1][j - 1] + 1;
        else
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
    }
}

时间复杂度

显而易见的，该算法的时间复杂度为 $O(N^2)$

输出序列

对于输出来说，我们只要将动态规划过程反过来，每次在遇到 dp[i][j] == dp[i - 1][j - 1] + 1 时候移动到 dp[i - 1][j - 1]，如果 s[i] == s[j]，那么我们将其加入输出序列；否则，在 dp[i - 1][j] 和 dp[j-1][i] 中会至少有一个和 dp[i][j] 相等，移动到相等位置即可。回到左上角后，便完成 $LCS$ 的输出

LCS 转化 LIS

对于 $LCS$ 问题，我们还可以将其转换为 $LIS$ 问题进行求解

对于下面两个序列 a = {a, d, c, e, b} 和 b = {a, c, d, b, e} 来说，我们将序列 b 做一个映射，将 b 中的值修改为 a 中对应数值的下标

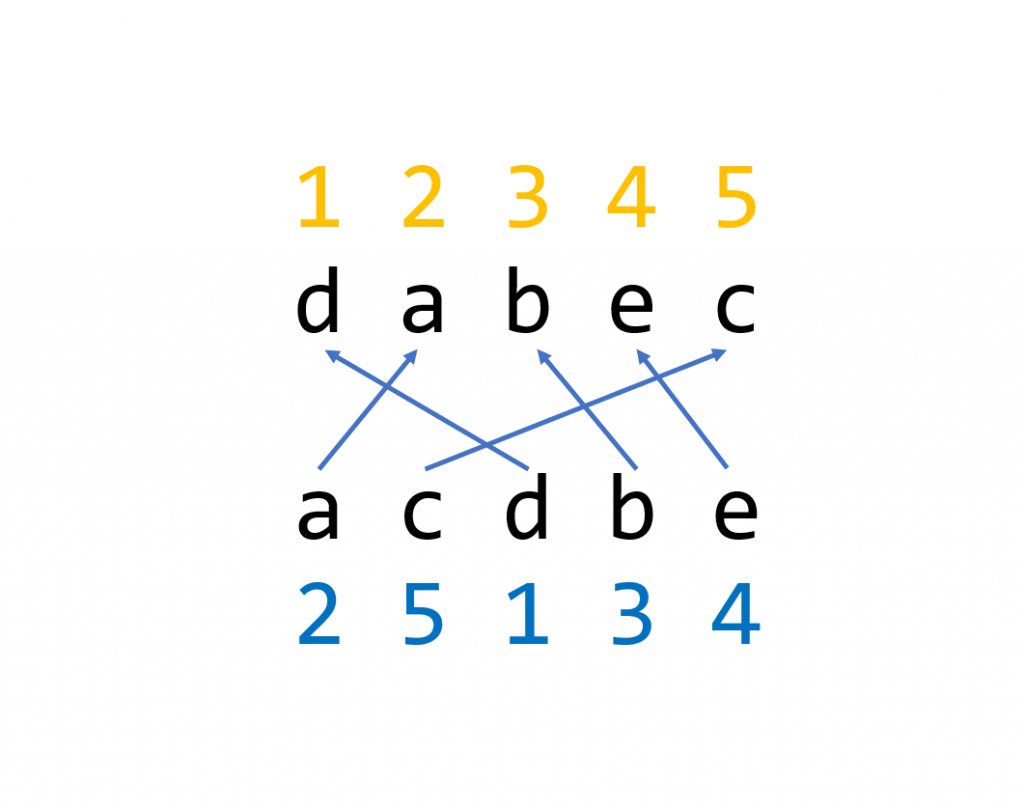
这样我们获得了两个新的序列：a = {1, 2, 3, 4, 5} 和 b = {2, 5, 1, 3, 4}

显然，在这种情况下，$LCS$ 的长度并没有改变。但是我们可以发现，对于两个序列的子序列来说，一定也是 a 的子序列，但是 a 本身是单调递增的！也就是说，子序列也是单调递增的

所以说，在 b 中的单调递增的子序列，都是 a 的子序列。那么最长的递增子序列自然就是 $LIS$ 啦

而对于有重复数值的序列，我们只要将它出现的位置递减排列，填入到每一个出现的位置即可；对于没有在另一个序列中出现的数值，我们直接不对其进行映射

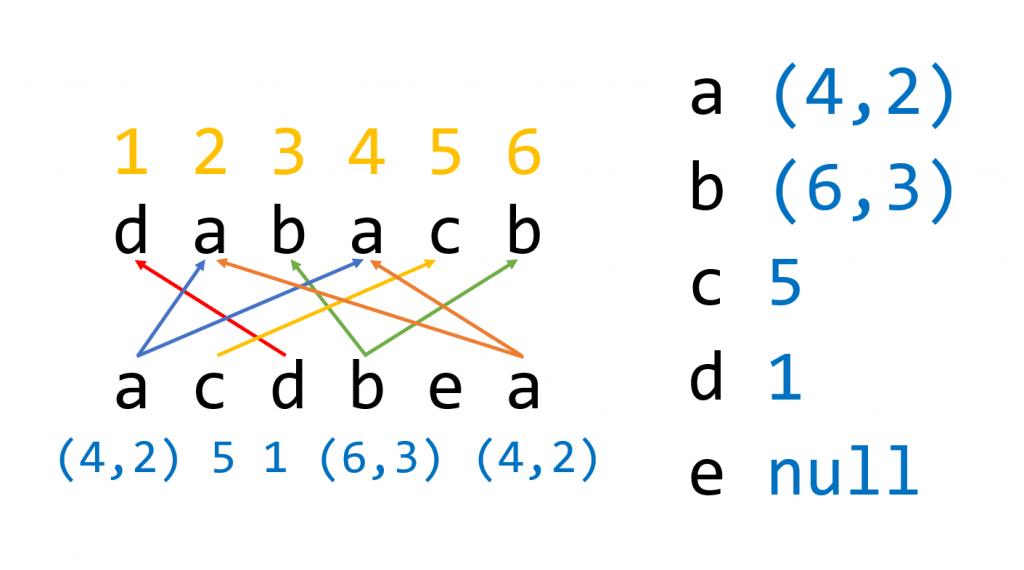
我们来看一道例题

例题

洛谷P1439 最长公共子序列

题意

给定两个长度为 $N$ 的全排列，求两个全排列的最长公共子序列长度 $(N \leq 10^5)$

思路

由于这道题的数据范围为 $N \leq 10^5$，所以朴素的 $O(n^2)$ 动态规划时间上会超时，所以我们这里将 $LCS$ 问题转化为 $LIS$ 问题

代码实现

int main()
{
    int n, t;
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        scanf("%d", &t);
        a[t] = i;
    }

    for (int i = 1; i <= n; ++i)
    {
        scanf("%d", &t);
        b[i] = a[t];
    }

    vector<int> v;
    v.push_back(b[1]);

    for (int i = 2; i <= n; ++i)
    {
        if (b[i] > *v.rbegin())
            v.push_back(b[i]);
        else if (b[i] < *v.rbegin())
            *upper_bound(v.begin(), v.end(), b[i]) = b[i];
    }

    cout << v.size() << endl;
    return 0;
}

时间复杂度

在一般情况下时间复杂度为 $O(n \log n)$，但是在极端情况下（比如两个序列中都是同一个字符）会退化为 $O(n^2 \log n)$