深度/广度优先搜索

深度优先搜索（DFS，Depth First Search）和 广度优先搜索（BFS, Breadth First Search）是在两种图中最基础也是最重要的算法

虽然它们都是用于遍历或是搜索图或树的算法，但是它们的用途完全不同，很少有混用两种算法的情况

DFS 也常指利用递归函数实现的暴力枚举的搜索算法，与图论中的 DFS 算法有一定的相似之处，但并不完全相同

深度优先搜索

深度优先搜索（DFS），顾名思义，也就是在每次都尝试向深层的节点走，在每次搜索时都优先访问下一层的节点，而不是同一层的节点，沿着一条道路走到底，如果发现不能达成目标解，才返回上一个节点选择另一条路

具体流程

对于如下的图来说，我们想使用 DFS 找到一条从 V1$\longrightarrow$V6 的路径

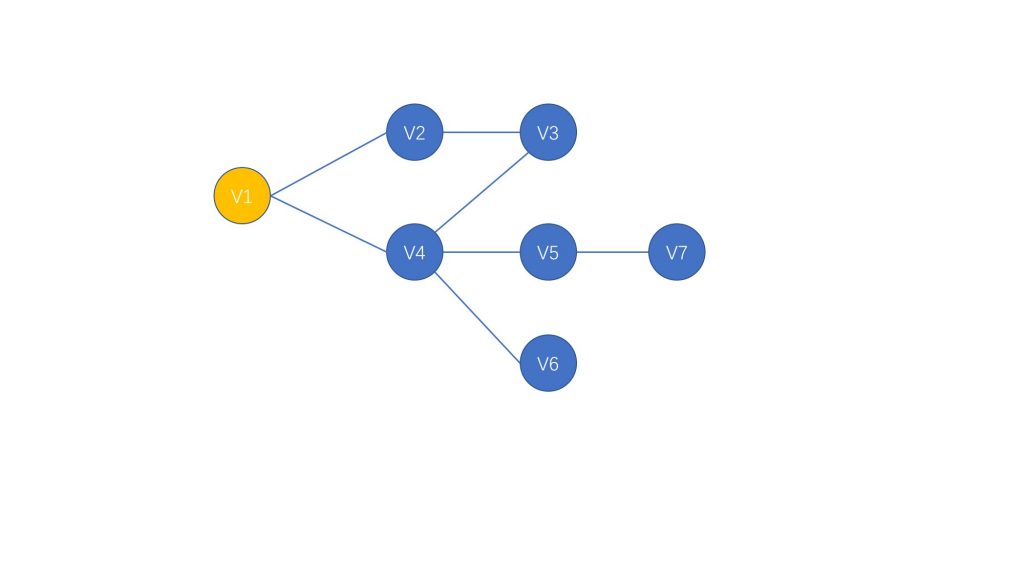
首先，我们寻找和 V1 节点连通的节点，随机选择一个节点进行搜索（一般在记录的表中靠前的节点会先被选中），这里我们选择 V2 节点进行第一次的搜索

所以，根据 DFS 的搜索方式，我们的第一次搜索的路径如下图：

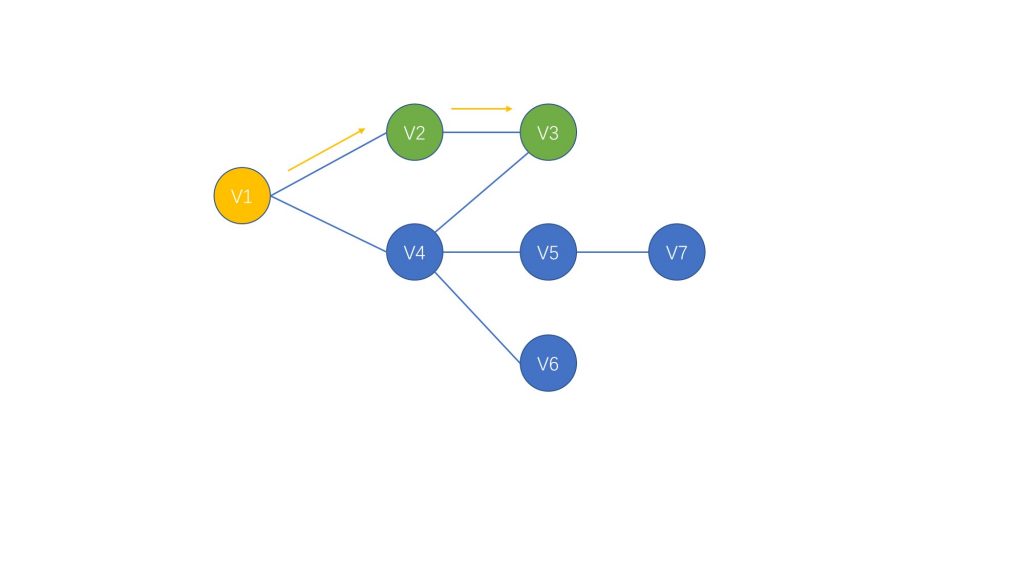
走到 V3 节点时，因为我们没有得到解（找到 V6 节点），并且 V3 节点不能再继续往下走，所以我们退回 V2 节点进行下一条路的搜索，但 V2 节点只有 V3 节点一个后继，我们已经走过，所以继续后退，回到 V1

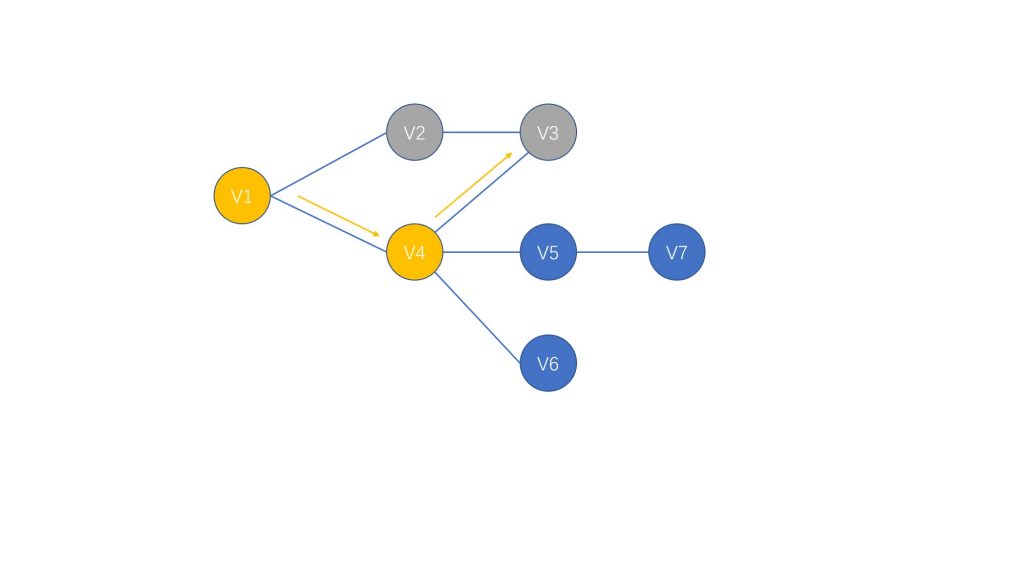
再次回到 V1 节点，这时我们已经访问过 V2 节点的所有路径，并且没有找到所需解，所以我们访问它的另一个后继 V4

在 V4 节点时，同我们刚刚在 V1 节点的操作，随机选择 V3 进行访问。这时因为我们已经将 V3 节点标记为已访问，所以直接退回 V4 节点

于是我们选择 V5 进行访问，并且我们的每一次访问都遵循着 优先访问下一层 的规则，所以我们第二次访问的路径如下：

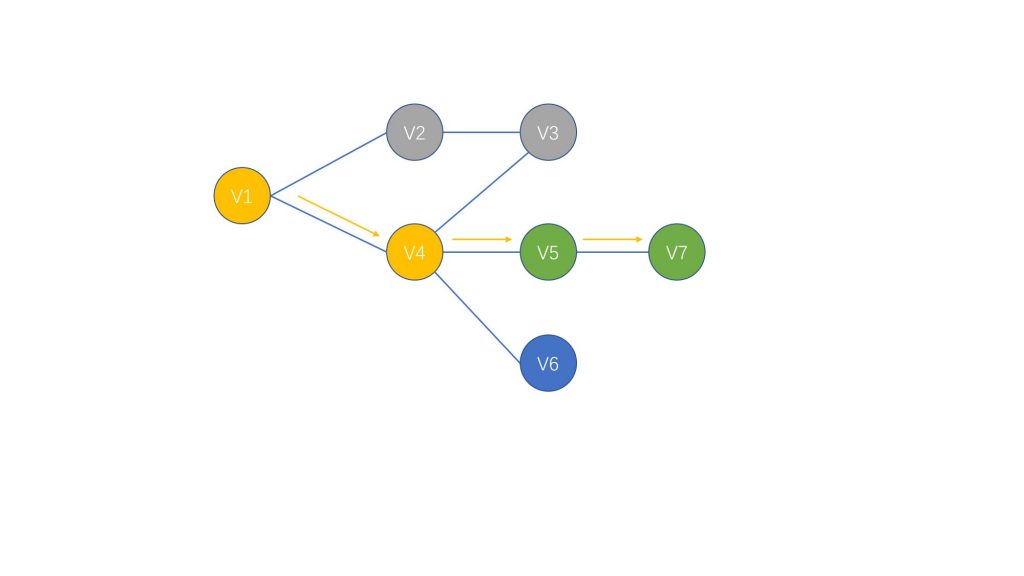
同样的，走到 V7 的时候，路走到了头并且没有找到所需的解，所以我们回退到 V4 并且访问它的另一个后继

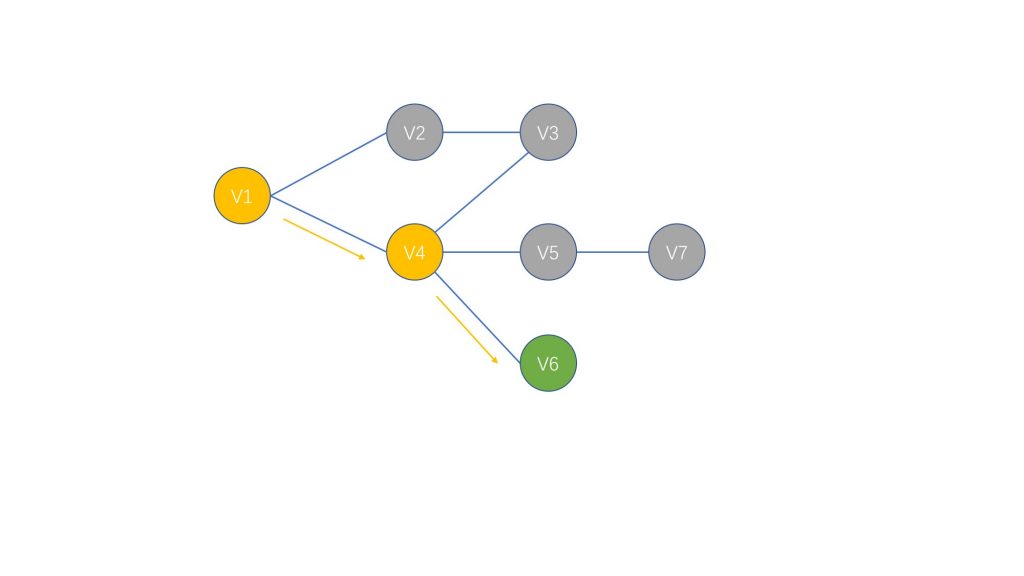
最后我们得到了 V1$\longrightarrow$V6 的路径

代码实现

以下代码基于链式向前星结构存图：

void dfs(int u)
{
    vis[u] = 1; // 标记节点已经访问过
    for(int i = head[u]; ~i; i = nxt[i]) // 遍历 u 的相邻节点
    {
        if(!vis[to[i]]) // 如果没有打过访问标记
        {

            dfs(to[i]);
        }
    }
}

时间复杂度

DFS 算法通常的时间复杂度为 $O(n+m)$，空间复杂度为 $O(n)$（使用邻接矩阵时为 $O(n^2)），其中 $n$ 表示点数，$m$ 表示边数

广度优先搜索

广度优先搜索（BFS）和上面介绍的深度优先搜索正好相反，它不优先访问下一层的节点，而是优先访问同一层的节点，在同一层的节点都被访问完了，才访问下一层的节点

因为 BFS 算法的搜索方法，让使用这个方法找到的路径是从起点开始的 最短 合法路径，也就是这条路径包含最少的 边数

在 BFS 算法中，每个节点都是通过从起点到该点的 最短路径 访问的

具体流程

还是以这张图为例，不过这次我们引入一个队列

首先我们将起点加入队列之中

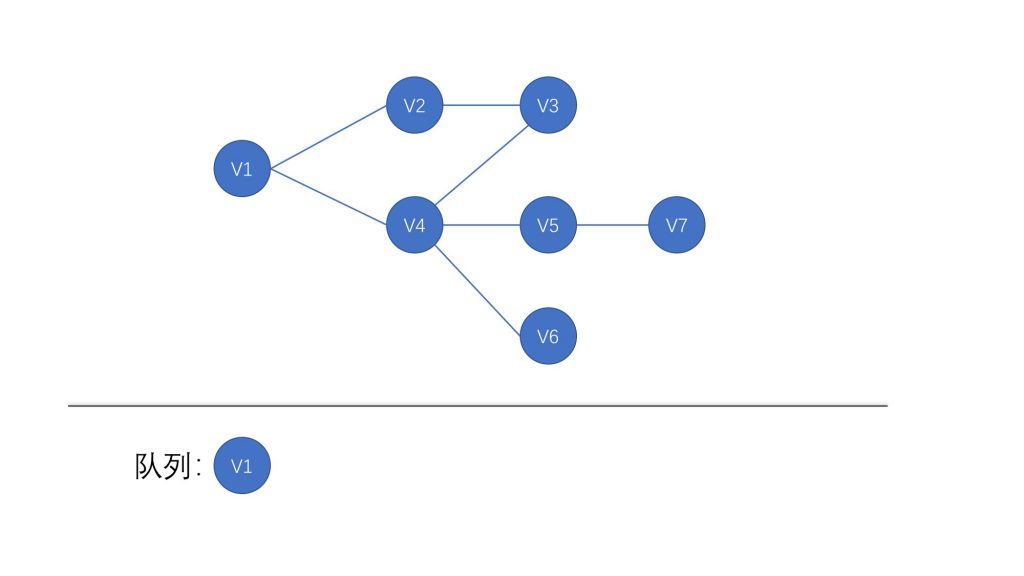
开始我们的 BFS 算法，每次我们从队列中取出第一个节点，将它的相邻节点加入到队列之中，所以在我们的第一次循环中，我们将 V2 和 V4 节点加入队列，并且将 V1 节点标记为已访问，然后继续从队列中取出第一个节点

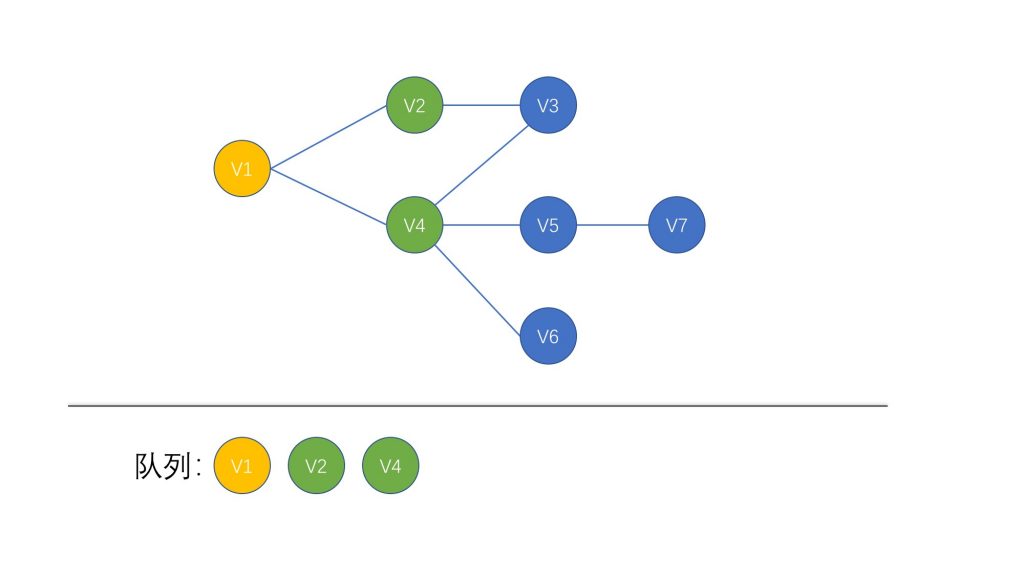
这时候队列中的第一个节点就变成了 V2 （因为 V1 已经被取出了），所以我们这次将 V2 节点取出，将它的相邻节点 V3 加入队列中

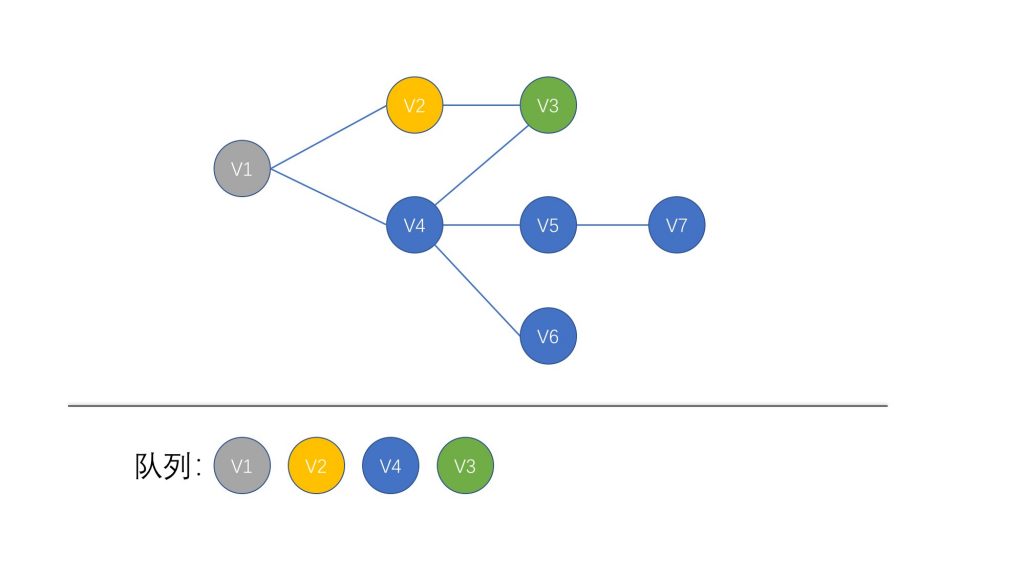
我们继续按照规则，将 V2 节点标记为已访问，取出 V4 节点并将它的相邻节点 V3、V5、V6 加入队列

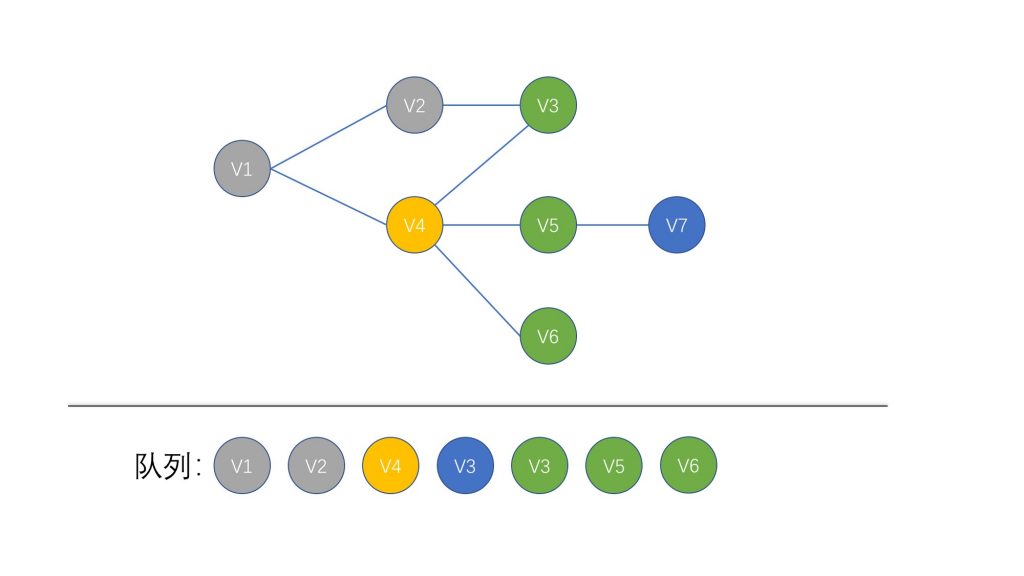
这时候我们发现，队列中有两个 V3 节点，好像要出现重复访问的问题，不过我们先耐下心继续往下看

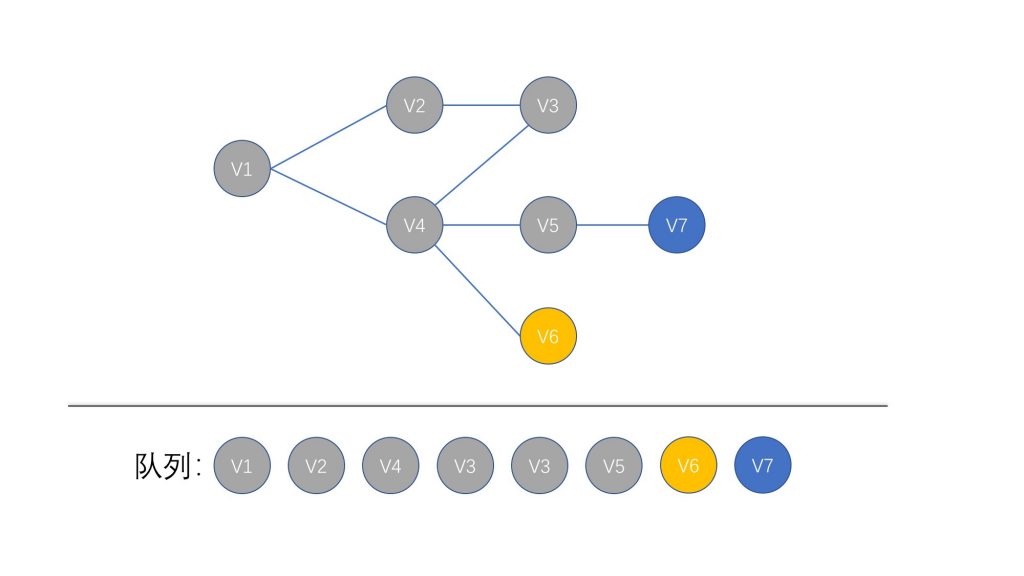
我们继续从队列中取出队首元素 V3，因为它没有 未访问的相邻节点，所以我们这次不添加任何节点进入队列中

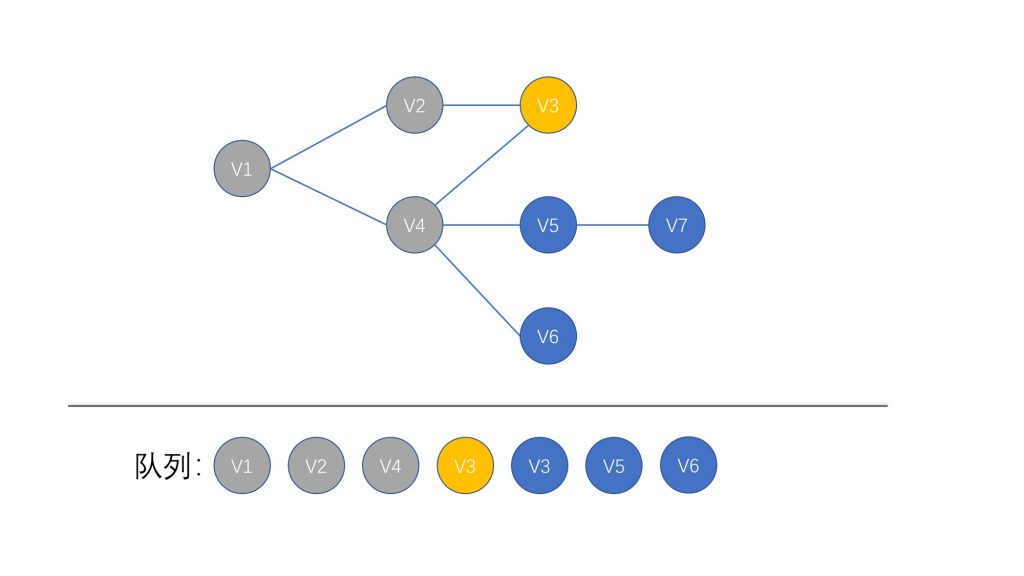
那么现在我们们取出队列中的第二个 V3 节点，由于之前的访问中，我们将 V3 节点标记为已访问的节点，所以这次并不会实际访问 V3 节点，而是直接跳过

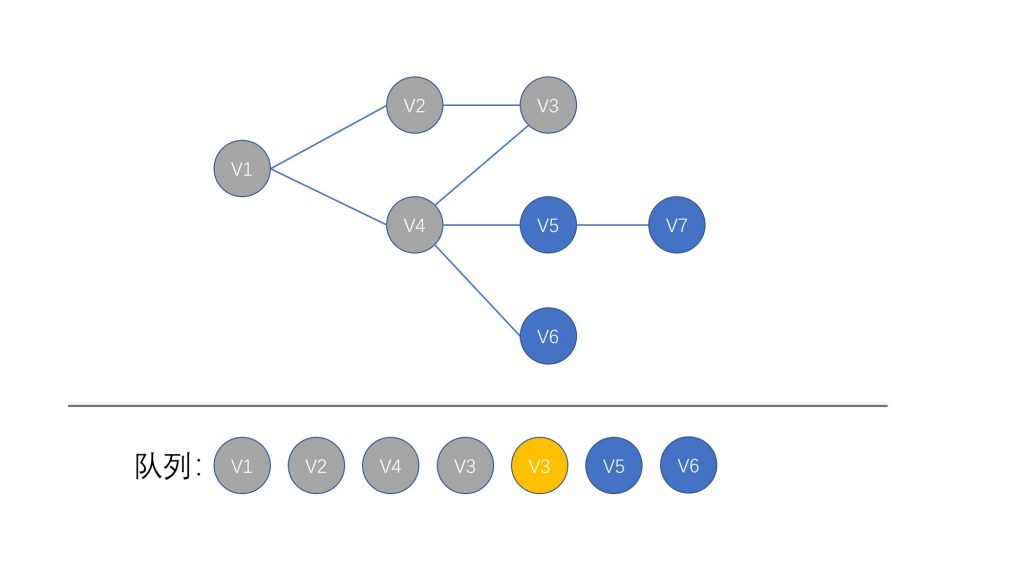
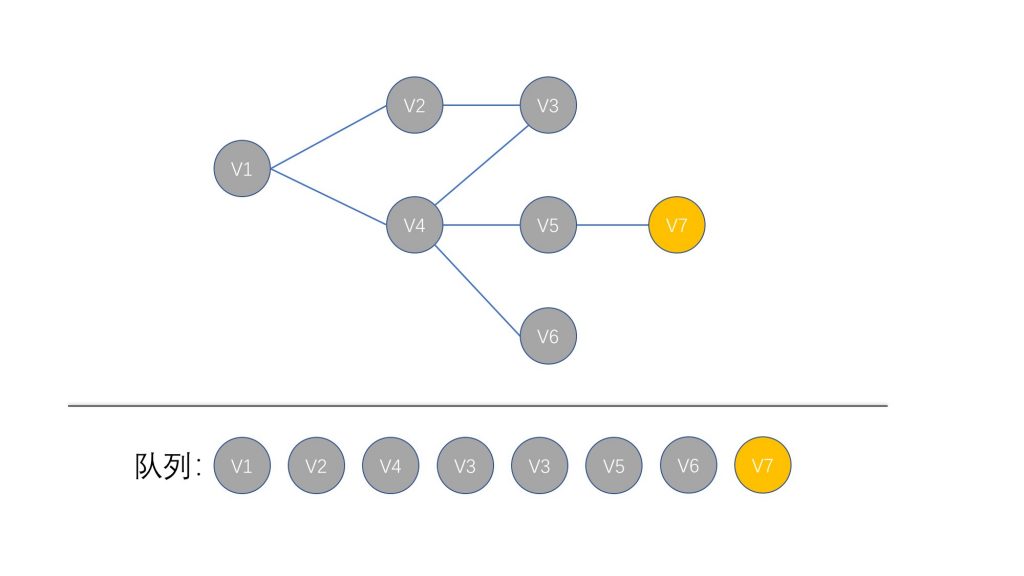
之后一直按照约定的规则，遍历整个图，完成整个 BFS

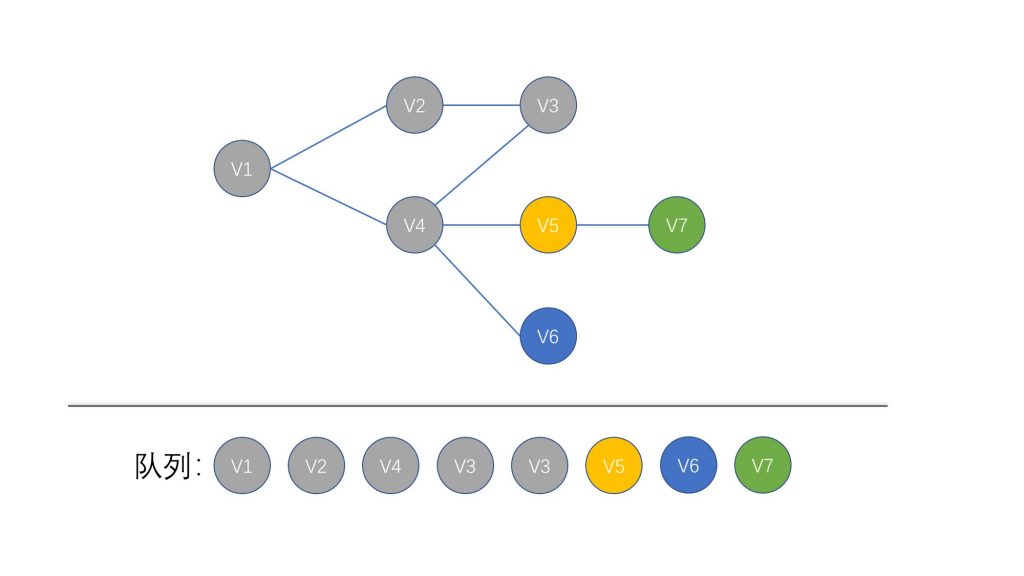
代码实现

以下代码同样基于链式向前星结构存图

void bfs(int u)
{
    while (!Q.empty())
        Q.pop();
    Q.push(u);
    vis[u] = 1;
    d[u] = 0;  // 标记起点到节点 u 的距离
    p[u] = -1; // 标记起点到节点 u 的最短路径
    while (!Q.empty())
    {
        u = Q.front(); // 取出队首元素
        Q.pop();
        for (int i = head[u]; ~i; i = nxt[i])
        {
            if (!vis[to[i]])
            {
                Q.push(to[i]);
                vis[to[i]] = 1; // 标记已访问过
                d[to[i]] = d[u] + 1;
                p[to[i]] = u;
            }
        }
    }
}

void restore(int x) // 用于还原上面 p 数组存储的最短路径
{
    vector<int> res;
    for (int v = x; v != -1; v = p[v])
    {
        res.push_back(v);
    }
    std::reverse(res.begin(), res.end());
    for (int i = 0; i < res.size(); ++i)
        printf("%d", res[i]);
    puts("");
}