快速幂 (Exponentiation by Squaring) 是一种简单高效计算乘方的小算法,它可以以 $O(log\ n)$ 的时间复杂度计算乘方。快速幂本身就是一种常见的算法,也常用于其他算法中
引入
让我们来思考一个问题:如何快速的计算 $6^{10}$
- Plan 1:回归初心,最朴素的做法,直接使用 10 个 6 相乘,共进行 9 次乘法
- Plan 2:先计算 6 的五次方 $6*6*6*6*6$,再计算它的平方,共进行 5 次乘法
Plan 1 无疑是过于缓慢的,对于现代 CPU 来说,每次乘一个小数,无疑是屈才
Plan 2 虽然快了许多,但对于 6 的五次方来说,还可以继续拆分,所以并不是最优解
所以我们引入Plan 3,先计算 $7 * 7 = 49$,再计算 $49*49*7$,然后计算它的平方,共进行 4 次乘法
模仿这样的过程,我们可以得出一个 $O(log \ n)$ 时间内计算幂的算法,也就是快速幂
递归快速幂
上面展示的,无疑是一个 二分 的思路,所以我们可以得到以下的一个方程
$$
\begin{equation}
x^n = \left\{
\begin{aligned}
x^{n-1} * x& , & if\ n\ is\ odd \\
x^{\frac{n}{2}} * x^{\frac{n}{2}} & , & if\ n\ is\ even\ but\ not\ 0 \\
1 & , & if\ n = 0
\end{aligned}
\right.
\end{equation}
$$
递归快速幂的方法非常简单,将函数实现即可。在 $n$ 为奇数的情况下,计算 $x^{n - 1}$ 再与 $x$ 相乘;在 $n$ 为偶数的情况下,计算 $x^{\frac{n}{2}}$ 再平方;递归的出口就是 $n=0$ 时的 1
int qpow(int x, int n)
{
if(!n)
return 1;
if(n & 1) // n & 1 和 n % 2 等价
return x * qpow(x, n - 1);
else if
{
int temp = qpow(x, n / 2);
return temp * temp;
}
}
注意,在这段代码中的temp是必须的,因为如果不使用temp进行保存,那么将会进行两次qpow(x, n / 2)运算,算法会退化为 $O(n)$
非递归快速幂(二进制快速幂)
递归版本的程序固然简洁容易理解,但是会产生对栈空间的大量占用
所以,我们引入非递归版本的快速幂,来避免对空间的额外占用
我们还是用 $6^{10}$ 来举例,但这次我们将 $10$ 写成二进制的形式 $(1010)_{2}$
现在我们要计算 $6^{(1010)_{2}}$,我们可以很容易的将它拆分为 $6^{(1000)_{2}} \cdot 6^{(10)_{2}}$
实际上,对于任意的整数,我们都可以把它拆成若干个 $6^{(10…)_{2}}$ 的形式相乘(因为对于任何一个十进制的自然数都能用二进制来表示它),所以这些值将恰好是 $6^{1}, 6^{2}, 6^{4} ……$,我们只要不断的将底数平方就能求出它们
int qpow(int x, int y)
{
int ans = 1;
while(y)
{
if(y & 1) // 如果二进制形式的最后一位为1
ans *= x;
x *= x;
y >>= 1;
}
return ans;
}
初始时 ans = 1,然后我们将幂次分解成二进制,一步一步计算
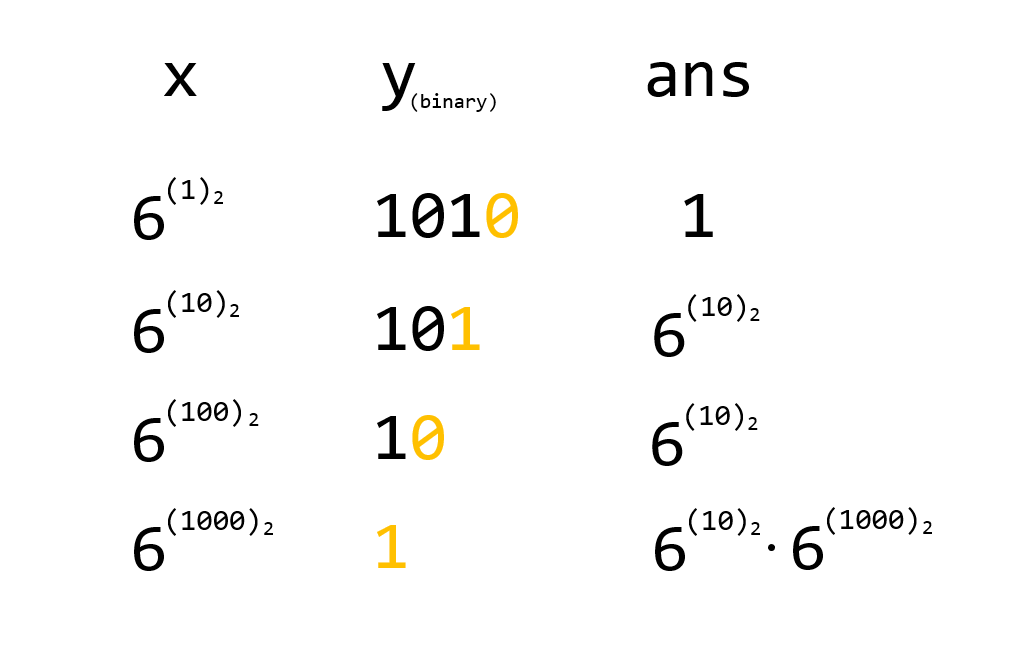
这种方法极大的减少了时间复杂度,可以在 $\lfloor\log_{2}{N}\rfloor$ 的时间复杂度下完成计算
矩阵快速幂
矩阵快速幂利用了矩阵乘法的结合律(其实,只要底数的乘法遵循结合律,底数可以是任意数据类型),将问题的递推式转化为矩阵的”等比数论”,然后使用快速幂求解递推式
我们来看最经典的一个使用矩阵快速幂来求解的问题:斐波那契数列
我们都知道,斐波那契数列的递推式是$ f(n) = f(n-1) + f(n-2) $
那么,我们创建矩阵 $A = \left[ \begin{array}{c} 0 & 1 \\ 1 & 1 \end{array} \right] $ 矩阵 $\left[ \begin{array}{c} F_n \\ F_{n+1} \end{array} \right]$
我们可以发现,有 $ A \left[ \begin{array}{c} F_n \\ F_{n+1} \end{array} \right] = \left[ \begin{array}{c} F_{n+1} \\ F_n + F_{n+1} \end{array} \right] = \left[ \begin{array}{c} F_{n+1} \\ F_{n+2} \end{array} \right]$
也就是说:
$$
\begin{array}{c}
\left[ \begin{array}{c} F_n \\ F_{n+1} \end{array} \right] & = & A \left[ \begin{array}{c} F_{n-1} \\ F_n \end{array} \right]\\
& = & A^2 \left[ \begin{array}{c} F_{n-2} \\ F_{n-1} \end{array} \right]\\
& = & A^3 \left[ \begin{array}{c} F_{n-3} \\ F_{n-2} \end{array} \right]\\
& & \cdots \\
& = & A^{n - 2} \left[ \begin{array}{c} F_2 \\ F_3 \end{array} \right]\\
& = & A^{n - 2} \left[ \begin{array}{c} F_1 \\ F_2 \end{array} \right]\\
& = & A^{n - 1} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
\end{array}
$$
于是我们把问题转化为了求矩阵 $A$ 的幂,可以使用快速幂来求解了
struct matrix
{
ll a, b, c, d; // a b
matrix(ll a, ll b, ll c, ll d) : a(a), b(b), c(c), d(d){}; // c d
matrix operator*(const matrix &x) const
{
return matrix((a * x.a) % mod + (b * x.c) % mod,
(a * x.b) % mod + (b * x.d) % mod,
(c * x.a) % mod + (d * x.c) % mod,
(c * x.b) % mod + (d * x.d) % mod);
}
};
matrix qpow(ll t, matrix y)
{
matrix ret(1, 0, 0, 1);
while (t)
{
if (t & 1)
ret = ret * y;
y = y * y;
t >>= 1;
}
return ret;
}
int main()
{
ll n;
cin >> n;
matrix a(0, 1, 1, 1);
matrix ans = qpow(n - 1, a); // 只需要乘 n-1 次
cout << ans.d % mod << endl;
return 0;
}



