Manacher算法

Manacher算法，又称“马拉车”算法，是一个可以在线性 $O(n)$ 内求出 字符串中每一个位置的回文半径 的算法

Manacher算法由 Glenn K. Manacher 在 1975 年提出，最初用于求解字符串中最长回文子串的长度

对于回文串来说，可以根据其长度分为奇回文串和偶回文串两种，也就是说 "abcba" 和 "abba" 均为回文串，而前者为奇回文串，后者为偶回文串

对于奇回文串来说，我们可以通过以一个字符为对称中心，向两边扩展的方法来很容易的得到它的长度，而对于偶回文串来说，我们似乎没有一种好的方法来快速的获取它的长度

所以，我们对原字符串做一个预处理，在字符串的两端和每两个相邻字符间加入一个 '#'（或者你喜欢的其他字符），那么，对于奇回文串 "abcba" 来说，变为 "#a#b#c#b#a#" 后，其对称中心不变；而对于偶回文串 "abba" ，变为以 '#' 为对称中心的奇回文串 "#a#b#b#a#"，这样我们就可以使用对付奇回文串的方法来统计偶回文串了

我们设 $d[i]$ 为以 $s[i]$ 为中心的最长回文串的半径，那么，最长的一个回文串的长度就是 $d[i] - 1$，而Manacher算法的作用，就是能在 $O(n)$ 内求出这个 d[ ] 数组

算法实现

Manacher算法维护一个 $l\leq i，r$ 最右的奇回文串，并在我们顺序枚举 $i$ 时，分成以下两个大类进行讨论：

$i > r$ 时

直接向两边扩展，暴力计算 $d[i]$ 并更新 $l, r$

$i \leq r$ 时

我们设 $sp$ 为 $i$ 关于我们维护的奇回文串 $s[l:r]$ 的对称点，那么将会有以下两种情况：

以 $sp$ 为中心的奇回文串的左边界大于 $l$

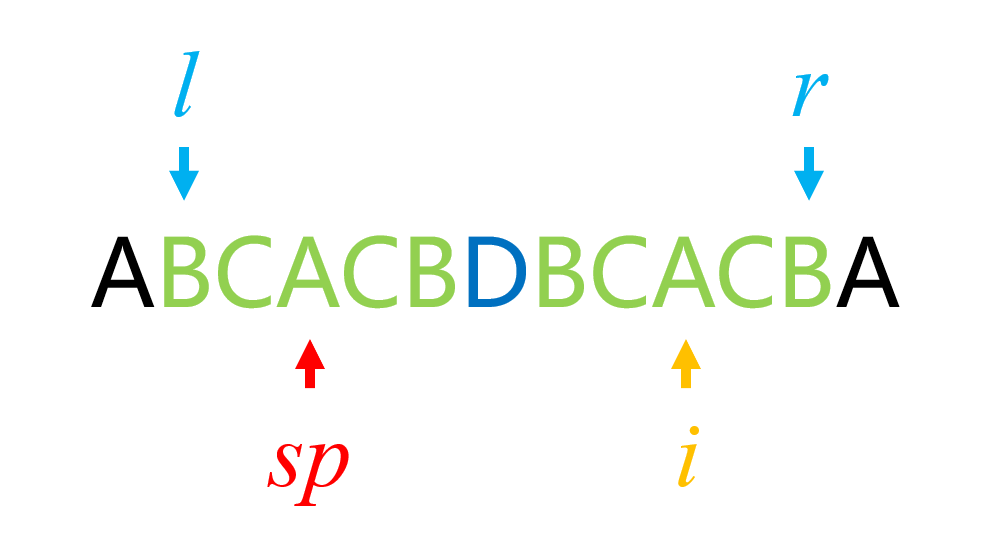
这时我们直接令 $d[i] = d[sp]$ 即可

以 $sp$ 为中心的奇回文串的左边界小于等于 $l$

这时我们无法第一时间确定回文串的长度（因为不知道两边还有没有延伸），但我们可以知道，$d[i]$ 至少有 $r - i + 1$ 长，所以我们令 $d[i] = r - i + 1$，再从这开始跑暴力的搜索

代码实现

vector<int> manacher(string &in)
{
    string s = "#";
    for(auto c : in) // 预处理字符串
    {
        s += c;
        s += '#';
    }
    int len = s.length();
    vector<int> d(len); // d[i]数组
    for(int i = 0, l = 0, r = -1; i < len; ++i)
    {
        int sp = l + r - i; // 对称点
        if(i > r) // 如果 i 在 r 右边，也就是第一种情况
        {
            while(i - d[i] >= 0 && i + d[i] < len && s[i - d[i]] == s[i + d[i]]) // 暴力匹配
                d[i]++;
            l = i - d[i] + 1, r = i + d[i] - 1;
        }
        else if(sp - d[sp] + 1 > l) // 对应第二种情况，m > l 时
        {
            d[i] = d[sp];
        }
        else // 对应第二种情况，m < l 时
        {
            d[i] = r - i + 1;
            while(i - d[i] >= 0 && i + d[i] < len && s[i - d[i]] == s[i + d[i]]) // 暴力匹配
                d[i]++;
            l = i - d[i] + 1, r = i + d[i] - 1;
        }
    }
    return d;
}

上面的循环可以简化为更短的版本

for(int i = 0, l = 0, r = -1; i < len; ++i)
{
    int t = l + r - i, sp = t >= 0 ? d[t] : 0;
    d[i] = max(min(sp, r - i + 1), 1); // 直接取对应点和 r - i + 1 中比较大的
    if(sp - d[sp] < l) // 除了 m > l 的情况，剩下都需要跑一定程度的暴力
    {
        while(i - d[i] >= 0 && i + d[i] < len && s[i - d[i]] == s[i + d[i]])
            d[i]++;
        l = i - d[i] + 1, r = 1 + d[i] - 1;
    }
}

最终代码如下

vector<int> manacher(string &in)
{
    string s = "#";
    for (auto c : in) // 预处理字符串
    {
        s += c;
        s += '#';
    }
    int len = s.length();
    vector<int> d(len); // d[i]数组
    for (int i = 0, l = 0, r = -1; i < len; ++i)
    {
        int t = l + r - i, sp = t >= 0 ? d[t] : 0;
        d[i] = max(min(sp, r - i + 1), 1); // 直接取对应点和 r - i + 1 中比较大的
        if (sp - d[sp] < l)                   // 除了 m > l 的情况，剩下都需要跑一定程度的暴力
        {
            while (i - d[i] >= 0 && i + d[i] < len && s[i - d[i]] == s[i + d[i]])
                d[i]++;
            l = i - d[i] + 1, r = 1 + d[i] - 1;
        }
    }
    return d;
}

时间复杂度

不难发现，每次循环都会将 $i++$，而 $r$ 只通过 $i$ 进行更新，所以在过程中 $r$ 为单调递增，算法时间复杂度为 $O(n)$