线段树(Segment Tree)是算法竞赛中常用的数据结构,主要用于维护 区间信息
线段树是一颗 平衡二叉树,它将长度大于 $1$ 的线段分为 左右两个区间,递归执行,从而把整个线段划分成为一个树形结构。在树中,每一个节点都是一个 区间,父节点代表了其下的 整个区间
要注意的是,虽然树中每一个节点都是一个区间,但并不保证 所有的区间 都是线段树的节点。对于任意区间,我们可以在树中找到一个 节点的集合 来代表它
它可以在 $O(\log n)$ 的时间下完成 区间修改(加、乘等)、区间查询(求和、查询大小值)等操作
它对比树状数组更具通用性(普通树状数组主要是 单点修改和区间查询)
线段树的构建
如下线段树是由数组 a[5] = {1, 3, 5, 7, 9} 构成:
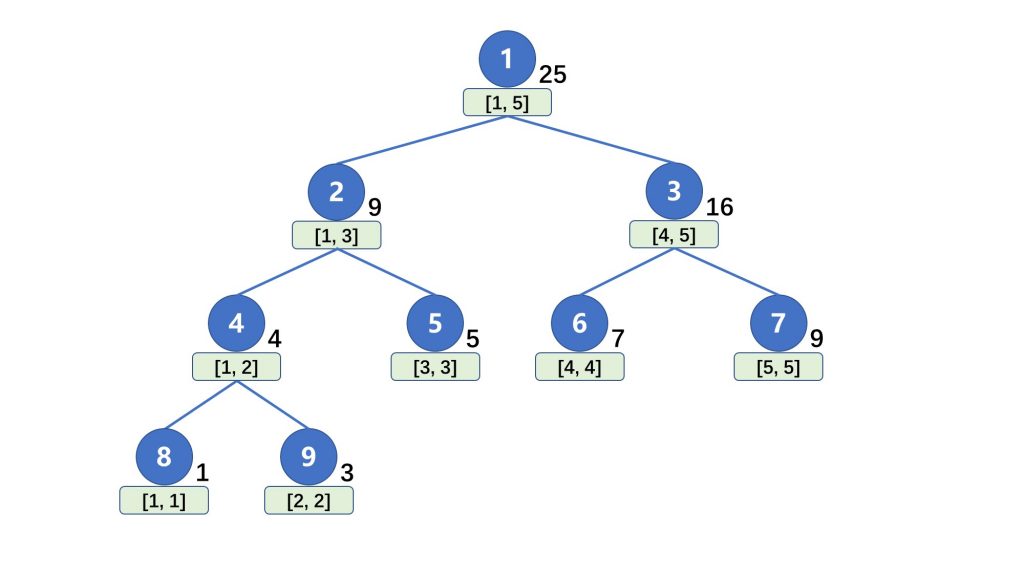
我们使用一个 $tree[\ ]$ 数组来保存线段树,设根节点的编号为 $1$ ,那么对于树中的节点 $p$ ,它的左右孩子分别是 $2p$ 和 $2p + 1$。当节点 $p$ 存储区间 $[l, r]$ 的和时,设 $mid = \dfrac{l+r}{2}$ ,那么节点 $2p$ 存储的是区间 $[l, mid]$ 的和,节点 $2p+1$ 存储的是区间 $[mid + 1, r]$ 的和
因为线段树是一颗平衡二叉树,所以我们可以得知:左节点的区间长度,和右节点相同或是多 $1$
我们可以用 递归 的方法建立这样一颗线段树:当 $l = r$ 时(也就是节点的区间长度为 $1$ 时),我们从数组中读取相应位置的值。否则,我们从区间的中点将它一分为二,分别递归建立左右两边的子树,最后在合并两个子节点的信息
(此处应有gif)
void build(ull l, ull r, ull p = 1)
{
if (l == r) // 如果相等,代表区间长度已经为 1
tree[p] = array[l]; // 直接赋值
else
{
ull mid = (l + r) >> 1;
build(l, mid, p << 1); // 递归建立左右子树
build(mid + 1, r, p << 1 | 1); // p << 1 | 1 等价于 p * 2 + 1
tree[p] = tree[p << 1] + tree[p << 1 | 1]; // 合并两个子节点的值
}
}
区间修改
懒惰标记
对于线段树的区间修改来说,朴素的做法是一层层的递归来进行修改,但这样的做法时间复杂度比较高
所以,我们引入线段树的精髓所在 —— 懒惰标记
对于每一个节点来说,懒惰标记是它的 子节点要更新的值(当前节点已经通过标记更新过)。所以,我们每次修改时,对于正好是区间的那些节点,我们不继续往下递归,而是给它打上这样一个标记,等到将来用得上它的 子区间 时,才继续向下传递
区间加
对于每次更新,我们都是从最大的区间开始,递归向下处理
我们以区间加为例(线段树的大部分操作都是这个思路)
目标区间为 $[l, r]$,当前区间为 $[cl, cr]$,当前节点为 $p$,需要修改的值为 $v$
那么,对于当前区间来说,有下面的三种情况:
目标区间和当前区间不相交
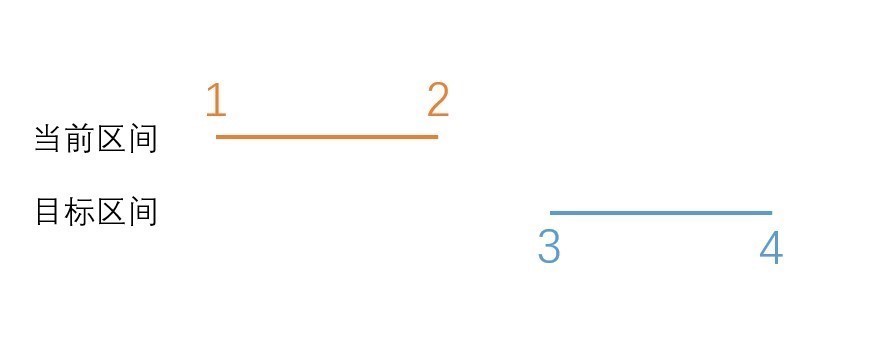
对于这种情况来说,我们只需要单纯的结束递归即可
if (cr < l cl > r) // 区间不相交
return; // 直接返回,剪枝
目标区间包含当前区间
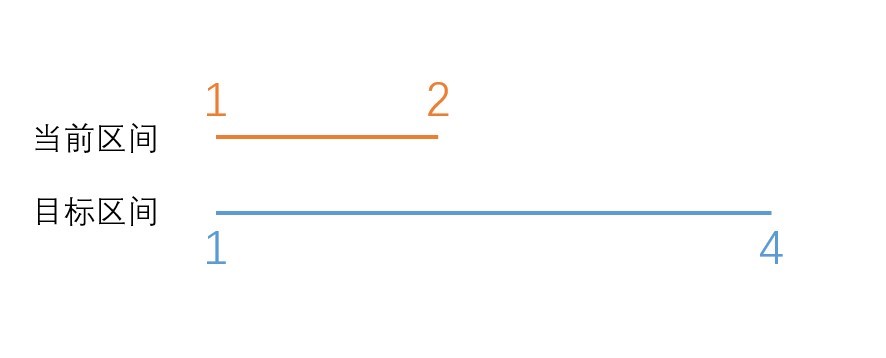
这时我们就要更新当前区间的值,并且更新当前区间的标记(因为我们并不会用到下面的节点,所以它的子节点不用更新标记)
else if (cr <= r && cl >= l) // 当前区间在目标区间里面
{
tree[p] += v * (cr - cl + 1); // 更新当前区间的值(cr - cl + 1 是区间的长度)
tag[p] += v; // 更新当前区间的标记
}
当前区间和目标区间相交,但不包含于其中
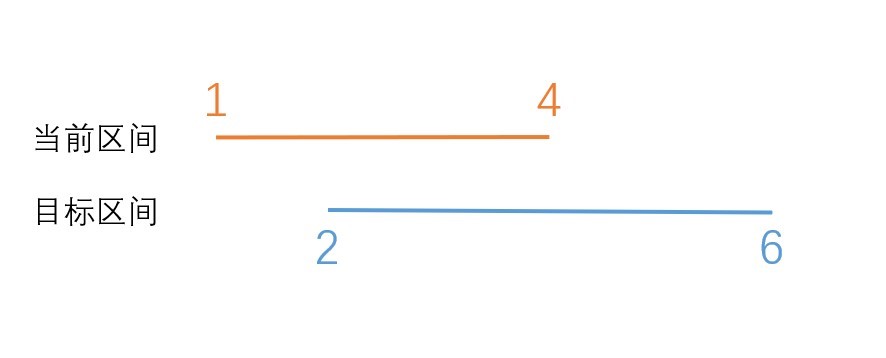
在这种情况下,我们将区间二分处理,如果存在懒惰标记的话,我们要首先将懒惰标记传递给子节点。然后,相应的更新两个子节点的值。最后,我们要 清除 当前节点的懒惰标记(已经传下去了嘛)
对于传递操作来说,我们并不会递归的进行传递,而是只向下传递一层(不然时间复杂度又上去了),等需要用上时在进行传递
else // 区间相交不包含
{
ll mid = (cl + cr) >> 1;
// 标记向下传递
tag[p << 1] += tag[p];
tag[p << 1 | 1] += tag[p];
// 更新子节点
tree[p << 1] += tag[p] * (mid - cl + 1);
tree[p << 1 | 1] += tag[p] * (cr - mid); // 在线段树中,右边的区间有可能比左边短
//清除当前节点标记
tag[p] = 0;
add(l, r, v, cl, mid, p << 1); // 更新左区间
add(l, r, v, mid + 1, cr, p << 1 | 1); // 更新右区间
tree[p] = tree[p << 1] + tree[p << 1 | 1]; // 更新区间的值
}
我们将向下传递标记的代码写成一个函数,方便之后调用
void push_down(ll p, ll len)
{
// 标记向下传递
tag[p << 1] += tag[p];
tag[p << 1 | 1] += tag[p];
// 更新子节点
tree[p << 1] += tag[p] * (len - (len >> 1));
tree[p << 1 | 1] += tag[p] * (len >> 1); // 在线段树中,右边的区间有可能比左边短
//清除当前节点标记
tag[p] = 0;
}
最终代码如下:
// 加法
void push_down(ll p, ll len)
{
// 标记向下传递
tag[p << 1] += tag[p];
tag[p << 1 | 1] += tag[p];
// 更新子节点
tree[p << 1] += tag[p] * (len - (len >> 1));
tree[p << 1 | 1] += tag[p] * (len >> 1); // 在线段树中,右边的区间有可能比左边短
//清除当前节点标记
tag[p] = 0;
}
void add(ll l, ll r, ll v, ll cl = 1, ll cr = n, ll p = 1)
{
if (cr < l cl > r) // 区间不相交
return; // 直接返回,剪枝
else if (cr <= r && cl >= l) // 当前区间在目标区间里面
{
tree[p] += v * (cr - cl + 1); // 更新当前区间的值
tag[p] += v; // 更新当前区间的标记
}
else // 区间相交不包含
{
ll mid = (cl + cr) >> 1;
push_down(p, cr - cl + 1); // 向下传递标记操作
add(l, r, v, cl, mid, p << 1); // 更新左区间
add(l, r, v, mid + 1, cr, p << 1 | 1); // 更新右区间
tree[p] = tree[p << 1] + tree[p << 1 | 1]; // 更新区间的值
}
}
区间乘
区间乘和区间加的思路一样,使用一个标记来存储其下节点需要乘的数值
唯一的区别是,区间乘的标记数组需要初始化为 1
// 乘法
void push_down(ll p, ll len)
{
// 标记向下传递
tag[p << 1] *= tag[p];
tag[p << 1 | 1] *= tag[p];
// 更新子节点
tree[p << 1] *= tag[p];
tree[p << 1 | 1] *= tag[p]; // 在线段树中,右边的区间有可能比左边短
//清除当前节点标记
tag[p] = 0;
}
void mult(ll l, ll r, ll v, ll cl = 1, ll cr = n, ll p = 1)
{
if (cr < l cl > r) // 区间不相交
return; // 直接返回,剪枝
else if (cr <= r && cl >= l) // 当前区间在目标区间里面
{
tree[p] *= v; // 更新当前区间的值
tag[p] *= v; // 更新当前区间的标记
}
else // 区间相交不包含
{
ll mid = (cl + cr) >> 1;
push_down(p, cr - cl + 1); // 向下传递标记操作
add(l, r, v, cl, mid, p << 1); // 更新左区间
add(l, r, v, mid + 1, cr, p << 1 | 1); // 更新右区间
tree[p] = tree[p << 1] + tree[p << 1 | 1]; // 更新区间的值
}
}
区间加 & 区间乘
在区间加和区间乘同时实现的情况下,遵循先乘后加的原则去更新标记即可
void push_down(ll p, ll len)
{
// 标记向下传递
tagm[p << 1] = tagm[p] * tagm[p << 1] % mod; // 传递乘法标记
tagm[p << 1 | 1] = tagm[p] * tagm[p << 1 | 1] % mod;
taga[p << 1] = (taga[p << 1] * tagm[p] + taga[p]) % mod; // 传递加法标记,由于有乘法的作用,需要先计算乘法
taga[p << 1 | 1] = (taga[p << 1 | 1] * tagm[p] + taga[p]) % mod;
// 更新子节点
tree[p << 1] = (tagm[p] * tree[p << 1] % mod + (len - (len >> 1)) * taga[p] % mod) % mod;
tree[p << 1 | 1] = (tagm[p] * tree[p << 1 | 1] % mod + (len >> 1) * taga[p] % mod) % mod; // 在线段树中,右边的区间有可能比左边短
//清除当前节点标记
taga[p] = 0;
tagm[p] = 1;
}
// 加法
void add(ll l, ll r, ll v, ll cl = 1, ll cr = n, ll p = 1)
{
if (cr < l cl > r) // 区间不相交
return; // 直接返回,剪枝
else if (cr <= r && cl >= l) // 当前区间在目标区间里面
{
tree[p] = (tree[p] + v * (cr - cl + 1)) % mod; // 更新当前区间的值
taga[p] = (taga[p] + v) % mod; // 更新当前区间的加法标记
}
else // 区间相交不包含
{
ll mid = (cl + cr) >> 1;
push_down(p, cr - cl + 1); // 向下传递标记操作
add(l, r, v, cl, mid, p << 1); // 更新左区间
add(l, r, v, mid + 1, cr, p << 1 | 1); // 更新右区间
tree[p] = (tree[p << 1] + tree[p << 1 | 1]) % mod; // 更新区间的值
}
}
// 乘法
void mult(ll l, ll r, ll v, ll cl = 1, ll cr = n, ll p = 1)
{
if (cr < l cl > r) // 区间不相交
return; // 直接返回,剪枝
else if (cr <= r && cl >= l) // 当前区间在目标区间里面
{
tree[p] = tree[p] * v % mod; // 更新当前区间的值
tagm[p] = tagm[p] * v % mod; // 更新当前区间的乘法标记
taga[p] = taga[p] * v % mod; // 加法标记也要乘上这个数
}
else // 区间相交不包含
{
ll mid = (cl + cr) >> 1;
push_down(p, cr - cl + 1); // 向下传递标记操作
mult(l, r, v, cl, mid, p << 1); // 更新左区间
mult(l, r, v, mid + 1, cr, p << 1 | 1); // 更新右区间
tree[p] = (tree[p << 1] + tree[p << 1 | 1]) % mod; // 更新区间的值
}
}
区间查询
和区间修改的思路一样,我们很容易就能想出区间查询的写法
ll query(ll l, ll r, ll cl = 1, ll cr = n, ll p = 1)
{
if (cr < l cl > r) // 区间不相交
return 0; // 直接返回,剪枝
else if (cr <= r && cl >= l) // 当前区间在目标区间里面
return tree[p];
else // 区间相交不包含
{
ll mid = (cl + cr) >> 1;
push_down(p, cr - cl + 1); // 向下传递标记操作
return (query(l, r, cl, mid, p << 1) + query(l, r, mid + 1, cr, p << 1 | 1)) % mod; // 二分处理
}
}
线段树还能维护许多不同的数据,如区间最值等,在操作时要注意不同标记之间是否有奇怪的影响(如区间乘对加法的影响)



