最短路问题

最短路问题是图论中一个基础而又重要的问题，如下图，我们经常会想知道，图中某点到某点的路径最短是多少？

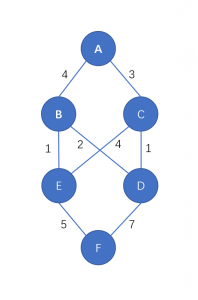
最短路问题分为两类，分别是 单源最短路 和 多源最短路。前者只需要求一个 固定的起点 到各个顶点的最短路径，后者则要求得出 任意两个结点 之间的最短路径

性质

1. 对于边权为正的图，任意两个结点之间的最短路，不会经过重复的 结点 和 边
2. 对于边权为正的图，任意两个结点之间的最短路，任意一条的结点数不会超过 $n$ ，边数不会超过 $n - 1$
3. 在有最短路径的图中，不存在负环

本文约定

在本文中，为了方便叙述，先与读者进行一些记号含义的约定

• $n$ 为图中点的数目，$m$ 为图中边的数目；
• $start$ 为最短路的起点；
• $D(u)$ 为 $start$ 点到 $u$点的 实际 最短路长度；
• $dis(u)$ 为 $start$ 点到 $u$ 点的 估计 最短路长度。任何时候都有 $dis(u)\ge D(u)$。特别的，当最短路算法终止时，应有 $dis(u)=D(u)$
• $w(u, v)$ 为边 $(u, v)$ 的 边权

Floyd 算法

Floyd算法是一种基于 动态规划 思想，用来求解 多源最短路 的算法，复杂度为 $O(n^3)$，但是常数项较小，且容易实现，适用于任何图（图中不存在 负环）

流程

我们定义一个三维数组 dis[k][x][y]，表示只允许经过图中结点 $1$ 到 $k$ 时 （$x$ 和 $y$ 不一定在其中），结点 $x$ 到 结点 $y$ 的最短路长度

所以，dis[n][x][y] 就是结点 $x$ 到结点 $y$ 的最短路长度（因为 $n$ 即为图里面所有点的数目，所以 dis[n][x][y] 就是允许经过图中所有结点时，$x$ 到 $y$ 的最短路长度）

那么，我们如何求出 dis[n][x][y] 的值呢？

我们首先考虑 dis[0][x][y] 的值：当 $x = y$ 时为零，因为到本身的距离为零；当 $x$ 和 $y$ 有直接相连的边时，为它们连接边的边权；当 $x$ 和 $y$ 之间没有直接相连的边的时候，为 $+\infty$（其实就是原图的 邻接矩阵）

dis[k][x][y] = min(dis[k-1][x][y]，dis[k-1][x][k] + dis[k-1][k][y])，dis[k-1][x][y] 为不经过 $k$ 点的最短路径；而 dis[k-1][x][k] + dis[k-1][k][y] 为经过 $k$ 点的最短路，求出它们两个中较小的那个即为允许经过点 $1-k$ 时的最短路长度

以下一次 Floyd 算法的实现过程：

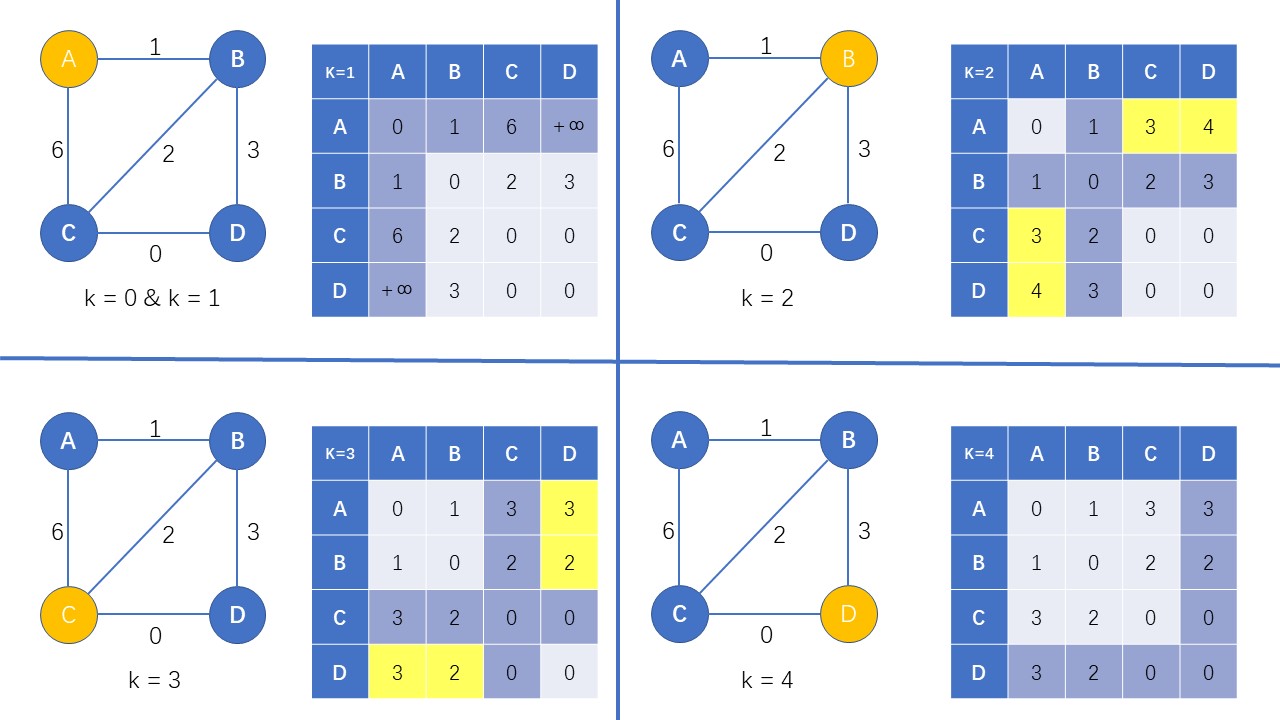
一开始 $k = 0$ 时，我们按照上面初始化 dis[0][x][y] 的方法初始化这张表格j

然后从 $k=1$ 开始计算，我们首先将点 $A$ 加入图中，计算可以通过点 $A$ 时，是否可以找到更短的路径长度

因为加入点 $A$ 并不能更新任何的路径，所以我们不对表格进行任何更改（这里偷懒让 $k = 0$ 和 $k = 1$ 使用同一份表格）

当 $k=2$ 时，我们将点 $B$ 加入，更新可以到达的最短路径，我们发现在加入点 $B$ 的情况下，点 $A$ 到点 $C$ 和点 $D$ 的最短路径可以更新，于是我们更新表中的对应位置

当 $k=3$ 和 $k=4$ 时重复以上操作，最后我们得到了一张包含图中所有点之间的最短路径长度的表格

算法实现

for(int k = 0; k < n; ++k)
{
    for(int x = 0; x < n; ++x)
    {
        for(int y = 0; y < n; ++y)
        {
            dis[k][x][y] = min(dis[k-1][x][y], dis[k-1][x][k] + dis[k-1][k][y]);
        }
    }
}

空间优化

通过上面的流程，我们注意到状态转移方程中 $dis[k][x][y] = min(dis[k-1][x][y], dis[k-1][x][k] + dis[k-1][k][y])$，即只与 $dis[k]$ 和 $dis[k-1]$ 有关，所以可以去掉数组中的第一维优化空间

dis[x][y] = min(dis[x][y], dis[x][k] + dis[k][y]);

复杂度

Floyd 算法的时间复杂度为 $O(n^3)$，空间复杂度为 $O(n^2)$

Bellman-Ford 算法

Bellman-Ford 算法是一种基于 动态规划 思想、使用 松弛（relax）操作来求解 单源最短路 的最短路算法，可以求出有 负权 的图的最短路，并可以判断最短路是否存在

下文将要介绍的 SPFA 算法就是 Bellman-Ford 算法的一种实现

流程

首先我们来了解松弛操作

对于边 $(u, v)$ ，使用式子 $dis(v) = min(dis(v), dis(u) + w(u, v))$ 进行松弛操作

换言之，松弛操作就是尝试使用 $start \leftarrow u \leftarrow v$（$start \leftarrow u$ 是其最短路径）这条路径去更新到点 $v$ 的最短路，如果这是更优的路径，就进行更新

Bellman-Ford 算法就是不断的尝试对图上的每一条边进行松弛操作，每进行一轮循环，就对图上所有的边尝试进行一次松弛操作。当在一次循环中没有成功的松弛操作时，算法终止

换言之，Bellmen-Ford 算法的大致流程如下：

1. 创建一个存储距离的数组并初始化，将起点的距离设置为 $0$，其他点设置为 $\infty$
2. 创建一个执行次数为 $n - 1$ 的循环
3. 在第二步的循环中，遍历每一条边，进行松弛操作

如下图，计算从点 $A$ 开始的到各个顶点的最短路长度：

由于 Bellman-Ford 算法执行的效率一定程度上取决于边存储的顺序，所以，为了不产生歧义，边的存储顺序在图中用标红圆圈给出

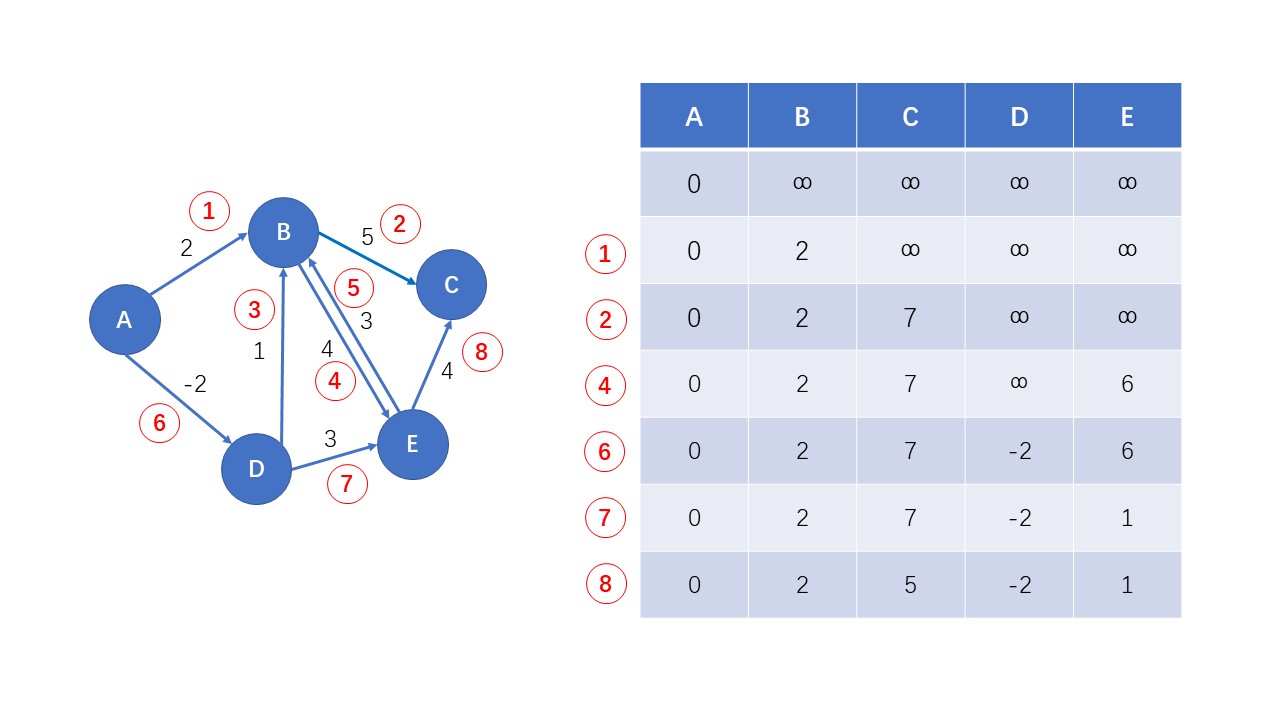
上图为 Bellman-Ford 算法执行完成第一次循环时的结果，之后循环参考第一轮循环

代码实现

下面的代码基于链式前向星存图：

int head[n], to[m], nxt[m], weight[m]; // 链式向前星存图
int dis[n];                            // 储存每个点当前的最短路径长度

bool bellmanFord(int n, int start)
{
    memset(dis, 63, sizeof(dis)); // 初始化为 +∞
    dis[start] = 0;
    bool flag = false;
    for (int i = 0; i < n; ++i)
    {
        flag = false;
        for (int u = 0; u < n; ++u)
        {
            for (int j = head[u]; ~j; j = nxt[j])
            {
                int v = to[j], w = weight[j];
                if (dis[v] > dis[u] + w) // 如果点 v 的最短路径大于点 u 的最短路径 + u -> v 的权重
                {
                    dis[v] = dis[u] + w; // 更新最短路径
                    flag = true;
                }
            }
        }
        if (!flag) // 没有可以松弛的边时就退出算法
            break;
    }
    return flag; // 如果执行完毕仍然可以松弛说明点 s 可以抵达一个负环
}

复杂度

在最短路存在的情况下，每轮循环至少会使得最短路的边数 $+ 1$，而前面提到过，最短路的边数不可能超过 $n - 1$，所以最多进行 $n-1$ 轮循环，因此时间复杂度为 $O(nm)$（每轮循环会遍历图中所有边，即 $m$）

用法

判断是否有负环

如果图中存在负环的话，松弛操作将永远成功，但是我们知道在存在最短路的情况下（即图中不存在负环），最多进行 $n-1$ 轮循环

所以我们只需加入一个与图上所有节点均链接一条权值为 $0$ 的边的点，然后以该点为起点执行 Bellman-Ford 算法，即可判断图中是否有负环（不建立一个这样的点的情况下，可能出现最短路径没有经过负环的情况）

SPFA 算法

SPFA 死了 SPFA 算法（Shortest Path Faster Algorithm)，是 Bellman-Ford 算法的一种优化

引入

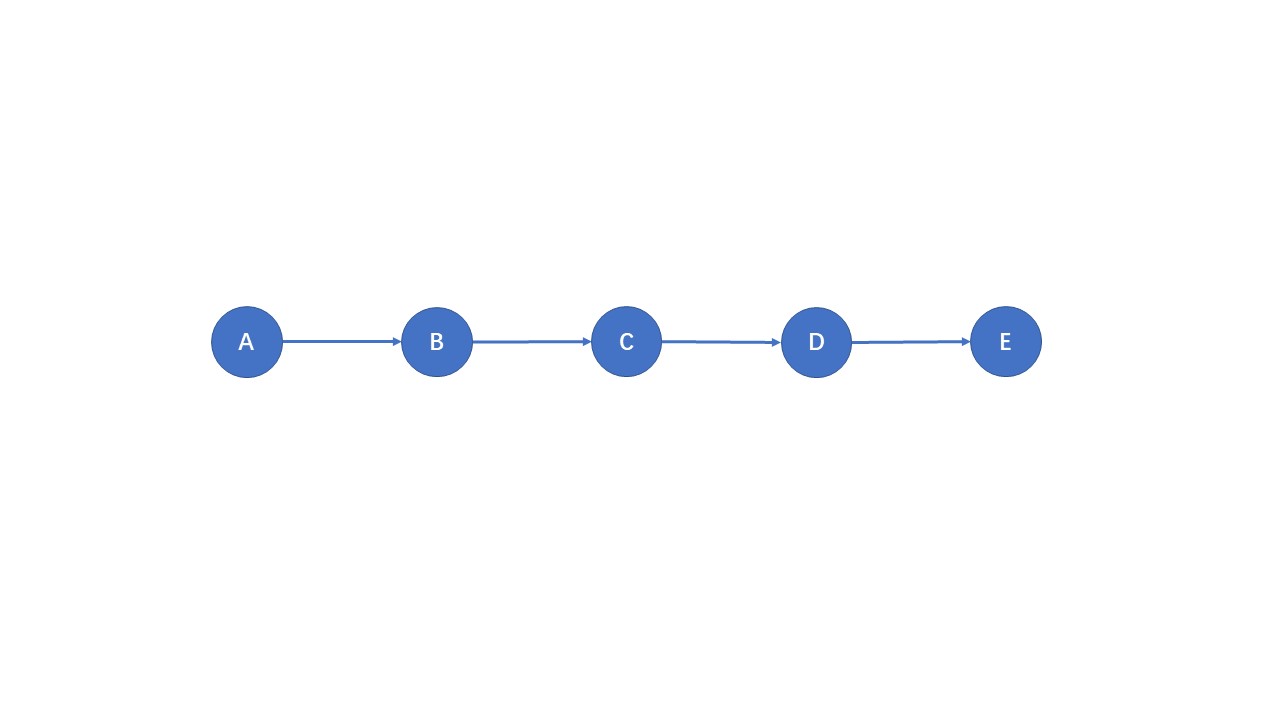
对于上图这样的有向图来说，使用 Bellman-Ford 算法进行最短路的计算时，每次都只有 一条边 贡献了有用的松弛操作，而在循环中却每次都对 所有边 进行了松弛操作。显然，在这种时候我们并不需要这些无用的松弛操作

流程

观察 Bellmam-Ford 算法的流程，不难看出，只有上一次被松弛的节点所连接的边，才可能进行下一次的松弛操作

那么，我们只需要引入一个队列来维护 可能引起松弛操作的节点，就可以舍弃那些不必要的操作了

在 SPFA 中，只需要加入一个数组，记录最短路经过了多少条边，即可用于判断起点是否可以抵达一个负环

代码实现

struct edge
{
    int v, w;
};

vector<edge> e[maxn];
int dis[maxn], cnt[maxn], vis[maxn];
queue<int> q;

bool spfa(int n, int s)
{
    memset(dis, 63, sizeof(dis));
    dis[s] = 0, vis[s] = 1;
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();
        q.pop(), vis[u] = 0;
        for (auto ed : e[u])
        {
            int v = ed.v, w = ed.w;
            if (dis[v] > dis[u] + w)
            {
                dis[v] = dis[u] + w;
                cnt[v] = cnt[u] + 1; // 记录最短路经过的边数
                if (cnt[v] >= n)
                    return false;
                // 在不经过负环的情况下，最短路至多经过 n - 1 条边
                // 因此如果经过了多于 n 条边，一定说明经过了负环
                if (!vis[v])
                    q.push(v), vis[v] = 1;
            }
        }
    }
    return true;
}

复杂度

在大多数情况下 SPFA 的速度很快，但是最坏情况下时间复杂度依然是 $O(nm)$，而且在大多数题目中都会随手把 SPFA 卡了给 SPFA 算法应有的尊重，所以在没有负权边时尽量使用 Dijkstra 算法

Bellman-Ford 的其他优化

除了队列优化（SPFA）之外，Bellman-Ford 还有其他形式的优化，这些优化在部分图上效果明显，但在某些特殊图上，最坏复杂度可能达到指数级

• 堆优化：将队列换成堆，与 Dijkstra 的区别是允许一个点多次入队。在有负权边的图可能被卡成指数级复杂度
• 栈优化：将队列换成栈（即将原来的 BFS 过程变成 DFS），在寻找负环时可能具有更高效率，但最坏时间复杂度仍然为指数级
• LLL 优化：将普通队列换成双端队列，每次将入队结点距离和队内距离平均值比较，如果更大则插入至队尾，否则插入队首
• SLF 优化：将普通队列换成双端队列，每次将入队结点距离和队首比较，如果更大则插入至队尾，否则插入队首
• D´Esopo-Pape 算法：将普通队列换成双端队列，如果一个节点之前没有入队，则将其插入队尾，否则插入队首

更多优化以及针对这些优化的 Hack 方法，可以看 fstqwq 在知乎上的回答

Dijkstra 算法

Dijkstra 算法由荷兰计算机科学家 E. W. Dijkstra 提出，是一种基于 贪心 思想，求解 非负权图 上单源最短路径的算法

流程

Dijkstra 算法将图分成两个部分，一部分是 已确定最短路长度 的点；另一部分是 未确定最短路长度 的点

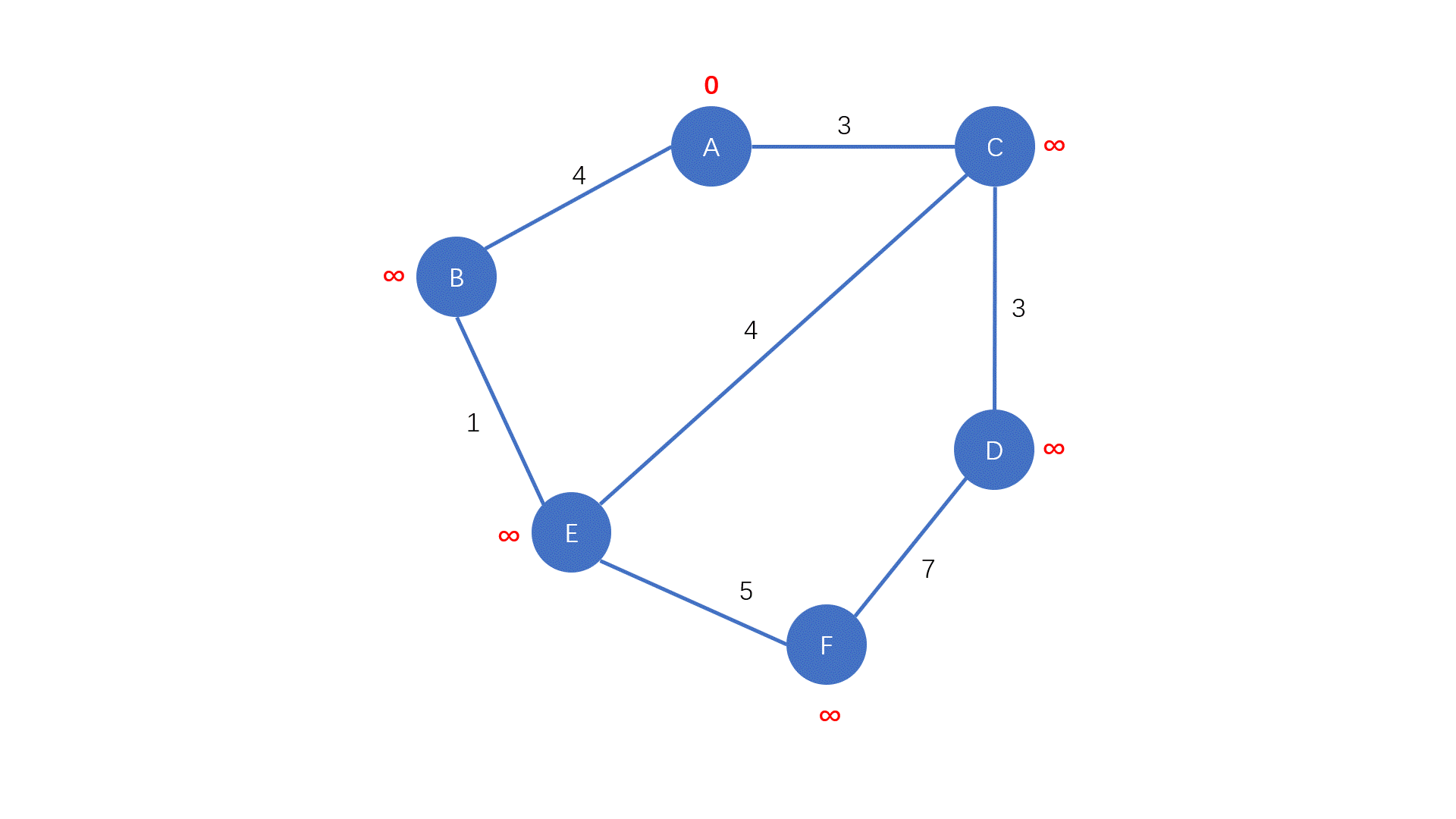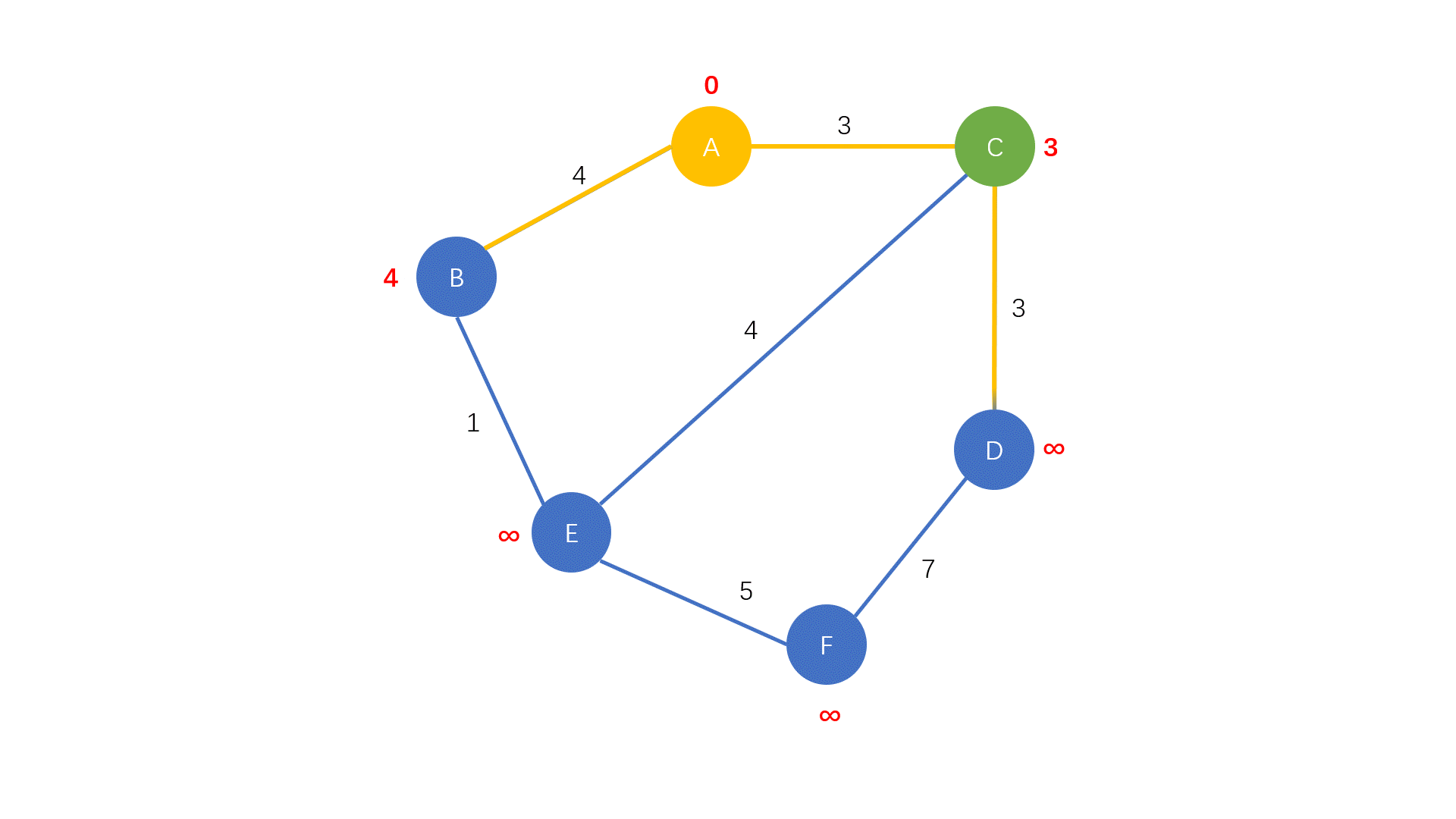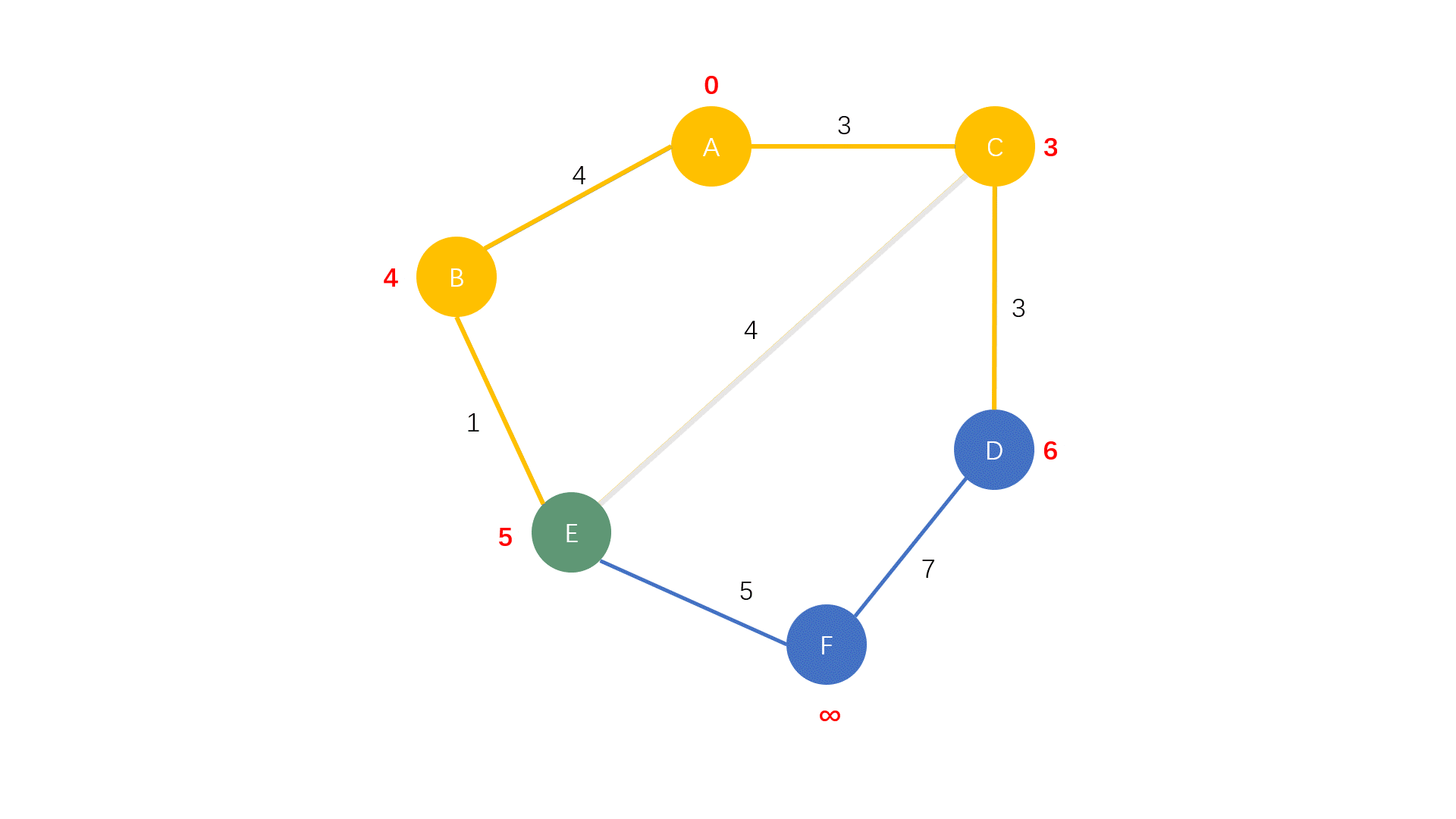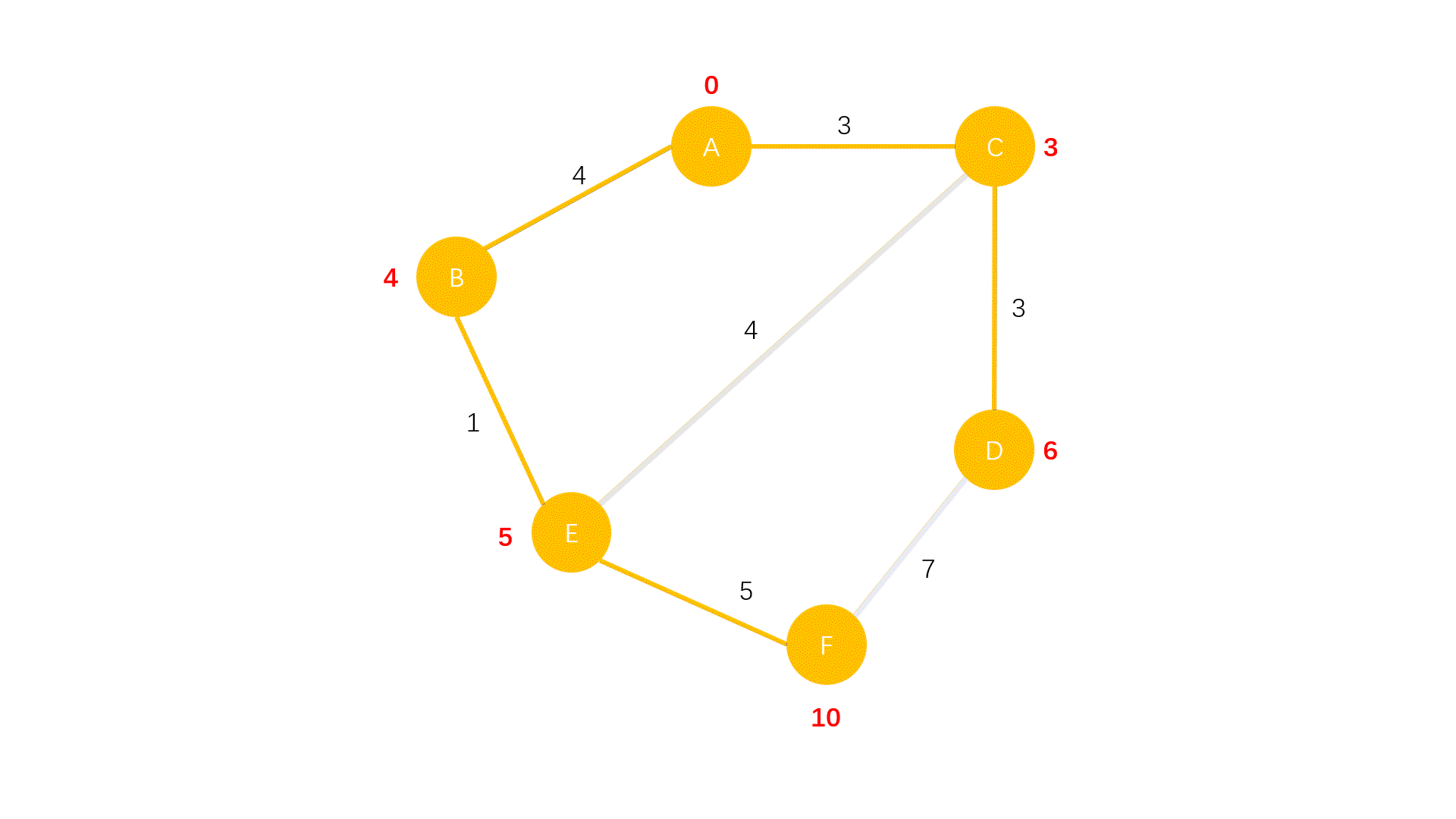
初始时我们将除 起点 外的所有点都归入 未确定最短路长度的点的集合中，并且初始化距离数组 $dis[start] = 0$，其余点均为 $+\infty$

这里使用 $U$ 代表未确定最短路长度的点的集合，使用 $D$ 代表已确定最短路长度的点的集合

然后按下面的流程重复执行：

1. 从 $U$ 中找出一个距离最近的点加入 $D$ 中
2. 对刚刚加入 $D$ 的点的所有出边进行松弛操作

当没有未确定最短路的点时，算法结束

代码实现

这里给出 $O(n^2)$ 的暴力做法和 $O(m \log m)$ 的优先队列做法的实现

// 暴力实现
struct edge
{
    int v, w;
};

vector<edge> e[maxn];
int dis[maxn], vis[maxn];

void dijkstra(int n, int s)
{
    memset(dis, 63, sizeof(dis));
    dis[s] = 0;
    for (int i = 1; i <= n; i++)
    {
        int u = 0, mind = 0x3f3f3f3f;
        for (int j = 1; j <= n; j++)
            if (!vis[j] && dis[j] < mind)
                u = j, mind = dis[j];
        vis[u] = true;
        for (auto ed : e[u])
        {
            int v = ed.v, w = ed.w;
            if (dis[v] > dis[u] + w)
                dis[v] = dis[u] + w;
        }
    }
}

// 优先队列实现
struct edge
{
    int v, w;
};

struct node
{
    int dis, u;

    bool operator>(const node &a) const { return dis > a.dis; }
};

vector<edge> e[maxn];
int dis[maxn], vis[maxn];
priority_queue<node, vector<node>, greater<node>> q;

void dijkstra(int n, int s)
{
    memset(dis, 63, sizeof(dis));
    dis[s] = 0;
    q.push({0, s});
    while (!q.empty())
    {
        int u = q.top().u;
        q.pop();
        if (vis[u])
            continue;
        vis[u] = 1;
        for (auto ed : e[u])
        {
            int v = ed.v, w = ed.w;
            if (dis[v] > dis[u] + w)
            {
                dis[v] = dis[u] + w;
                q.push({dis[v], v});
            }
        }
    }
}

时间复杂度

我们可以使用多种算法来维护上面操作中的最短路长度最小的点，不同的维护方式带来了不同的时间复杂度：

• 暴力：不使用任何数据结构进行维护，每次 2 操作执行完毕后，直接在 $U$ 集合中暴力寻找最短路长度最小的结点。2 操作总时间复杂度为 $O(m)$，1 操作总时间复杂度为 $O(n^2)$，全过程的时间复杂度为 $O(n^2 m)$
• 二叉堆：每成功松弛一条边 $(u,v)$，就将 $v$ 插入二叉堆中（如果 $v$ 已经在二叉堆中，直接修改相应元素的权值即可），1 操作直接取堆顶结点即可。共计 $O(m)$ 次二叉堆上的插入（修改）操作，$O(n)$ 次删除堆顶操作，而插入（修改）和删除的时间复杂度均为$O(\log n)$ ，时间复杂度为 $O((n+m) \log n) = O(m \log n)$
• 优先队列：和二叉堆类似，但使用优先队列时，如果同一个点的最短路被更新多次，因为先前更新时插入的元素不能被删除，也不能被修改，只能留在优先队列中，故优先队列内的元素个数是 $O(m)$ 的，时间复杂度为 $O(m \log m)$
• Fibonacci 堆：和前面二者类似，但 Fibonacci 堆插入的时间复杂度为 $O(1)$，故时间复杂度为 $(n \log n+m)$，时间复杂度最优。但因为 Fibonacci 堆较二叉堆不易实现，效率优势也不够大，算法竞赛中较少使用
• 线段树：和二叉堆原理类似，不过将每次成功松弛后插入二叉堆的操作改为在线段树上执行单点修改，而 1 操作则是线段树上的全局查询最小值。时间复杂度为 $O(m \log m)$

在稀疏图中，$m=O(n)$，使用二叉堆实现的 Dijkstra 算法较 Bellman-Ford 算法具有较大的效率优势；而在稠密图中，$m=O(n^2)$，这时候使用暴力做法较二叉堆实现更优

Johnson 全源最短路算法

Johnson 和 Floyd 一样，是一种能求出无负环图上任意两点间最短路径的算法。该算法在 1977 年由 Donald B. Johnson 提出

//TODO